前回、前々回の記事では振動の基本として減衰無し(不減衰)と減衰ありの
最も単純で一般的な場合での自由振動について説明しました。
前々回・前回
回転機械の振動 2-1.振動の基本-不減衰自由振動
回転機械の振動 2-2.振動の基本-減衰自由振動
今回はこれらの系に対して外力が加わった時の運動について説明します。
1自由度系の強制振動
急に1自由度という言葉が出てきましたが、これはこれまで説明してきたような
物体のx方向のみ(1方向のみ)の運動を考えるモデルのという意味なので、
あまり深く考えなくて大丈夫です。
ちなみに1自由度系のと書いていますが、この記事で2自由度以上の系に関する説明を
するつもりはありません。
さて、外力による振動と言いましたが、外力がF=Aの様な一定の力の場合、
これまで説明してきたような、ばねを持つ振動系ではばねと外力がつり合い、
ある位置で静止することになります。
もしくは物体に変形等が発生するかもしれませんが、
これらは振動学で扱う運動ではありません。
では、どのような外力を考えるかというと以下の様なものになります。
F=F_{0}cos\omega t
これはある振幅F_0で周期的に変動する外力で、
物体に対して直接作用します。
このような外力が具体的にどのような状況を表しているかというと、
例えば物体mの中にファンやモータが組み込まれており、
そのファン等が周波数ωで振動している場合です。
(この場合ωはファンやモータの回転数になるでしょう。)
強制振動の運動方程式
さて、では早速運動方程式を立てていきましょう。
物体に作用する力は減衰による力、ばねによる力、外力ですので
mx''=-cx'-kx +F_0 cos\omega t
となります。さらに移項して
\begin{equation}
m''+cx'+kx=F_0cos\omega t
\end{equation}これは線形非同次微分方程式になります。
線形微分方程式の解法については番外編で説明していますので、
もし必要な方はそちらを見てみてください。
回転機械の振動 番外編1. 微分方程式の解法
上の記事で説明しているように、線形非同次微分方程式の一般解は、
(右辺)=0とした線形同次微分方程式の一般解と
元の線形非同次微分方程式の特解を足したものになります。
(右辺)=0とした線形同次微分方程式の一般解は前回の記事で説明しており
\begin{equation}
x=C_1e^{-\zeta \omega _n t+\sqrt{\zeta ^2 -1}\omega_n t}+C_2e^{-\zeta \omega _n t-\sqrt{\zeta ^2 -1}\omega_nt}
\end{equation}C_1,C_2は定数,~\zeta = \frac{c}{c_c},~\omega_n = \sqrt{\frac{k}{m}},~c_c=2\sqrt{mk}となります。
ここから更に\zetaの値により振動運動となる場合と
振動しない場合に分かれますが、減衰が正であれば(通常考える減衰は正です)
どちらの場合でも時間とともに0に近づきます。
これに関しても前回の記事で説明しています。
回転機械の振動 2-2.振動の基本-減衰自由振動
場合分けはひとまず置いておいて、特解を求めていきたいと思います。
強制振動の特解
右辺に三角関数が入っている場合の特解は番外編のでも特解の求め方 例2として示しましたが、
再度特解を求めていきましょう。
特解Xを以下の様に仮定します。
X=Bcos \omega t+Csin\omega t
Xの1階微分、2階微分はそれぞれ
\begin{align*}
X'&=-B\omega sin \omega t+C\omega cos \omega t\\
X''&=-B\omega^2cos \omega t-C\omega ^2 sin \omega t
\end{align*}となるので、これらを式(1)にx=Xとして代入して
\begin{align*}
m(-B\omega^2cos \omega t-C\omega ^2 sin \omega t)+c(-B\omega sin \omega t+C\omega cos \omega t)+k(Bcos \omega t+Csin\omega t)&=F_0cos \omega t\\
(-mB\omega ^2+cC\omega +kB)cos \omega t+(-mC\omega ^2 -cB\omega+kC)sin\omega t&=F_0cos\omega t
\end{align*}これらの係数を比較して
\begin{align}
(-mB\omega ^2+cC\omega +kB)&=F_0\\
(-mC\omega ^2 -cB\omega+kC)&=0
\end{align}となるB,Cを求めます。式(4)を変形して式(3)に代入して
\begin{align*}
B&=\frac{-m\omega ^2 +k}{c\omega}C\\
(-m\omega ^2+k)B+cC\omega&=F_0\\
\frac{(-m\omega ^2+k)^2}{c\omega}C+cC\omega &=F_0\\
\frac{(-m\omega ^2+k)^2+c^2\omega ^2}{c\omega}C&=F_0\\
C&=\frac{c\omega}{(-m\omega ^2+k)^2+c^2\omega ^2}F_0\\
B&=\frac{-m\omega ^2 +k}{c\omega}×\frac{c\omega}{(-m\omega ^2+k)^2+c^2\omega ^2}F_0\\
&=\frac{-m\omega ^2 + k}{(-m\omega ^2+k)^2+c^2\omega ^2}F_0
\end{align*}
これより特解Xとして
X=\frac{-m\omega ^2 + k}{(-m\omega ^2+k)^2+c^2\omega ^2}F_0cos\omega t+
\frac{c\omega}{(-m\omega ^2+k)^2+c^2\omega ^2}F_0 sin\omega tが得られます。これを更に変形します。
X=\frac{F_0}{\sqrt{(-m\omega ^2+k)^2+c^2\omega ^2}}cos(\omega t-\phi)\\
~~~~~~~~\phi = tan^{-1}(\frac{C}{B})=tan^{-1}(\frac{c\omega}{-m\omega ^2+k})
この変形は不減衰自由振動の説明をした際にもしましたが、
その時には詳しく説明していなかったので一応記事末尾でおまけとして説明しておきます。
得られた式を
\nu=\frac{\omega}{\omega_n},~\omega_n=\sqrt{\frac{k}{m}}を用いて更に整理します。
\begin{align*}
X&=\frac{F_0}{\sqrt{(-m\omega ^2+k)^2+c^2\omega ^2}}cos(\omega t-\phi)\\
&=\frac{\frac{F_0}{k}}{\sqrt{(\frac{-m\omega ^2}{k}+1)^2+\frac{4mc^2\omega ^2}{4mk×k}}}cos(\omega t-\phi)\\
&=\frac{\frac{F_0}{k}}{\sqrt{(-\frac{\omega ^2}{\omega_n^2}+1)^2+\frac{4c^2\omega ^2}{c_c^2\omega_n^2}}}cos(\omega t-\phi)\\
&=\frac{\frac{F_0}{k}}{\sqrt{(-\nu^2+1)^2+4\zeta^2\nu^2}}cos(\omega t-\phi)\\
&=\frac{\frac{F_0}{k}}{\sqrt{(1-\nu^2)^2+(2\zeta\nu)^2}}cos(\omega t-\phi)\\~~\\
&\phi = tan^{-1}(\frac{C}{B})=tan^{-1}(\frac{c\omega}{-m\omega ^2+k})\\
&~~=tan^{-1}(\frac{c\omega\times\frac{2}{2\sqrt{mk}}\times\sqrt{\frac{m}{k}}}{(-m\omega ^2+k)\times\frac{1}{k}})\\
&~~=tan^{-1}(\frac{c\omega\times\frac{2}{c_c}\times\frac{1}{\omega_n}}{-\frac{m}{k}\omega ^2+1})\\
&~~=tan^{-1}(\frac{2\zeta\nu}{-\nu^2+1})=tan^{-1}(\frac{2\zeta\nu}{1-\nu^2})
\end{align*}ここでXの中に現れるF_0/kは外力の振幅F_0を
振動させずに作用させたときの変位量になります。
これをx_{st}とし、特解Xの振幅部分をx_0として、これらの比をとります。
M_f=\frac{x_0}{x_{st}}=\frac{1}{\sqrt{(1-\nu^2)^2+(2\zeta\nu)^2}}この比M_fを振幅倍率と呼びます。
強制振動の一般解と特解の意味
さて、ここまで特解Xにばかり注目してきました。
実際には物体の運動は一般解 式(2)と特解Xの和として
\begin{align*}
x=C_1e^{-\zeta \omega _n t+\sqrt{\zeta ^2 -1}\omega_n t}+C_2e^{-\zeta \omega _n t-\sqrt{\zeta ^2 -1}\omega_nt}+\frac{1}{\sqrt{(1-\nu^2)^2+(2\zeta\nu)^2}}\frac{F_0}{k}cos(\omega t-\phi)\\
C_1,C_2は定数,~\zeta = \frac{c}{c_c},~\omega_n = \sqrt{\frac{k}{m}},~c_c=2\sqrt{mk},\phi =tan^{-1}(\frac{2\zeta\nu}{1-\nu^2}),\nu=\frac{\omega}{\omega _n}
\end{align*}で表されます。
しかし、前述した通り正の減衰cが存在していれば、一般解の部分は時間とともに0に近づきます。
また減衰が小さい場合でも、初期に何らかの加振力がなければ初期位置からは動きません。
これらのことから通常、振動系の特性を評価する場合には特解Xの部分のみを評価します。
もちろん減衰が小さく、しかも初期に無視できない加振や振動運動が存在している場合は
これらを考慮して実際の振動問題を考えてください。
この場合でも基本的には一般解部分の自由振動と特解部分の重ね合わせなので、
以下の議論で得られる振動系の特性に関する知識はとても有用です。
周波数応答関数
これまでの説明で得られた振幅倍率M_fは周波数応答関数の一種です。
周波数応答関数というのはその名の通り、周波数に対する系の振動応答を表す関数です。
応答というとピンと来ないかもしれませんが、例えば振幅倍率M_fの分母x_st=F_0/kは
外力が振動的でない場合の物体の変位なので、これが1以上であるということは静的に外力を加えるよりも
振幅が大きくなり、より大きく応答しているということになります。
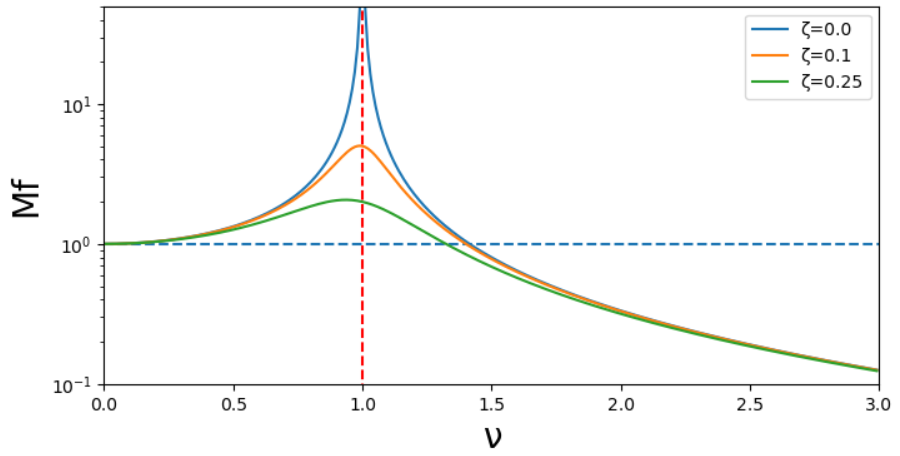
言葉で説明してもよくわからないと思いますので、先ほど得られたM_fをグラフにしてみましょう。

\zetaについていくつか値を変えてグラフを描いてみました。
\zeta=0,\nu = 1の時、M_f=\inftyになります。
\zeta=0というのは減衰c=0ということで、このとき振幅は無限に大きくなり続けます。
実際には現実世界に存在するほとんどのものに減衰が存在するので、
無限大になる前に有限のある振幅で落ち着くことになります。
ただし、ばねの伸びも有限なので、振幅が落ち着く前にばねの限界に到達すると
ばねが破断するなどして、機械が壊れてしまいます。
また、減衰が存在する場合でも\nu=1付近で応答が
大きくなっていることが分かります。
このような振動が大きく増幅される現象を共振と言い、このときの周波数を
系の「固有振動数」、「共振周波数」または単に「共振点」などと呼びます。
(厳密には使い分けがあるのかもしれませんが、
多くの場合ほぼ同じ意味として混同して使われます。
また、自身の回転数が加振力になる回転機械では、
「危険速度」と呼ばれることもあります。
振動数\omegaが共振周波数を超えると(\nu>1)、
振幅倍率M_fは小さくなっていき、\nu=\sqrt{2}(\simeq 1.41)を超えると1を下回ります。
共振と位相の関係
次に位相\phiについて見ていきましょう。
位相についても同様に\nuについてのグラフを描くことができます。
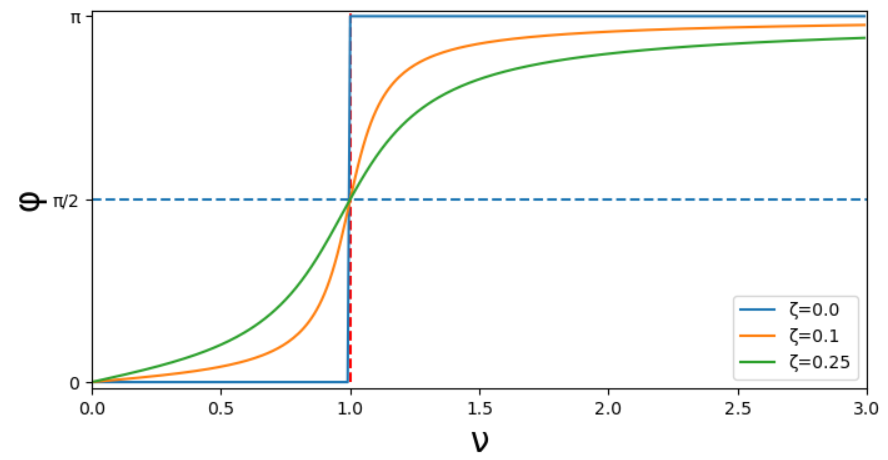
位相は\nuが小さいときには0ですが、徐々に大きくなり\nu=1付近では
\phi=\pi/2となり、その後更に大きくなって\piへと近づいていきます。
また、減衰が大きいほどなだらかな変化となっていることが分かります。
このグラフが何を示しているか、少し考えてみましょう。
このグラフが何を示しているか、少し考えてみましょう。
そもそも位相\phiが何を意味しているかというと、外力Fが
F=F_0cos\omega t
であるのに対して物体の運動xが
x=M_f\times F_0 cos(\omega t - \phi)
という同じ\omega tのcos関数で表されていることから、
位相\phiは外力と運動の時間方向のずれだと言えます。
実際にグラフで見てみましょう。
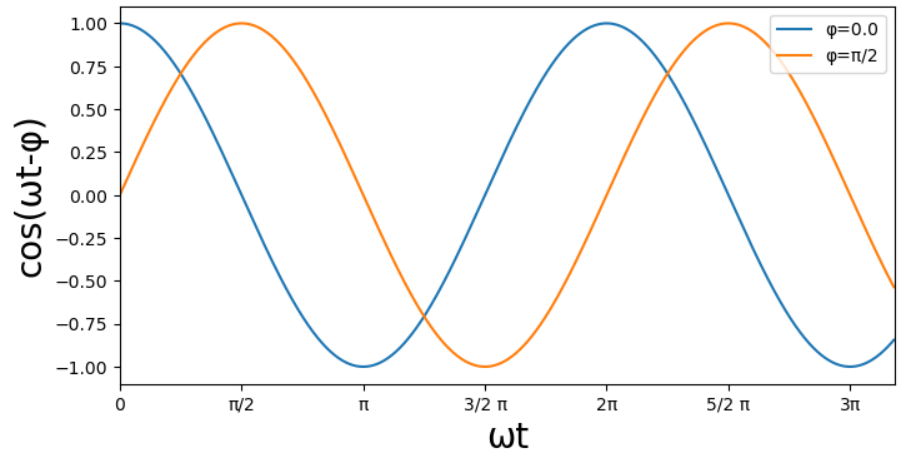
少しわかりにくいですが、右側ほど時間が後ですので、\phi = \pi/2の方が
\phi = 0.0の動きを遅れて追いかける形になっています。
このことから\phiは位相遅れと呼ばれます。
さて、ここで運動xの速度を考えてみましょう。速度は位置xの微分なので
\begin{align*}
x&=Acos(\omega t-\phi)\\
x'&=-A\omega sin(\omega t- \phi)
\end{align*}となります。
これを先ほどのグラフに記入してみます。(ωは適当に決めます。)
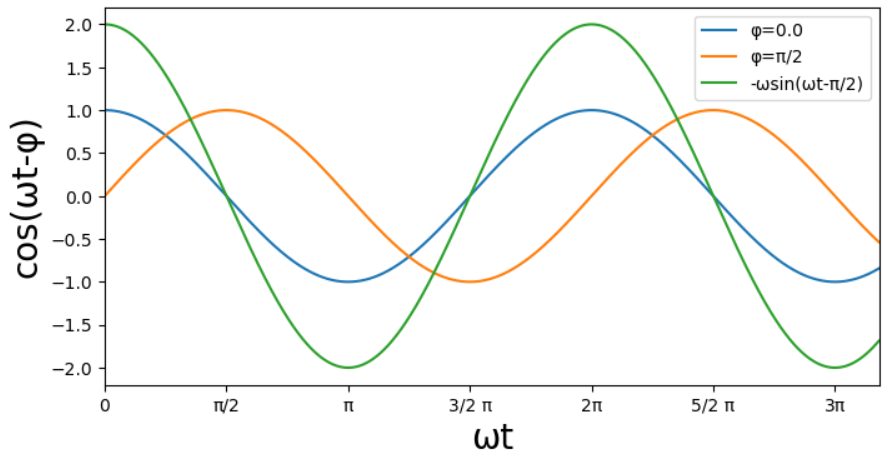
見てわかる通り、位相遅れ0(=外力)と速度の位相が一致しています。
つまり共振現象とは力のタイミングと、物体の速度のタイミングが一致するために
運動が成長し続ける現象ということです。
逆に言えば共振現象が発生しているとき、運動の位相は加振力に対して\pi/2遅れます。
これは物体の振動に関するとても基本的なことですが、意外と忘れがちなことです。
今後周波数応答を測定する方法など説明することがあるかもしれませんが、
その際に位相を観察することでその周波数が共振周波数であるかどうかを判断できます。
共振周波数よりも振動数が大きくなると位相が\pi~(=180°)ずれるため、
外力は常に運動と逆方向に作用するようになります。
これにより振幅倍率M_fは小さくなっていきます。
周波数応答関数の種類
これまで説明してきた通り、振幅倍率や位相は振動周波数によって大きく変化するため、
これらの周波数応答関数を知ることは系の特性を知るのにとても役立ちます。
今回紹介した振幅倍率は加振力、運動がともに変位で表される(変位)/(変位)の応答でしたが、
それ以外にも力に対する速度や加速度で表される場合もあります。
ここでは紹介しませんが、それぞれ特有の名前がついており、
それらすべて周波数応答関数となります。
(なので、周波数応答関数と言われただけではそれが(変位)/(変位)の関数とは限りません。)
また、周波数応答関数を縦軸に対数目盛を取って表したものをボード線図と言います。
縦軸に対数を取ることで広い範囲の応答を知ることができます。
伝達率
周波数応答関数によく似た考え方として伝達率があります。
これまで扱ってきた下図の系で、左側の壁が受ける力を考えてみましょう。

物体が運動する際、物体は壁からばねと減衰器を通じて力を受けます。
その時壁は物体からの反力として逆向きの力を受けています。
つまり壁は物体が振動しているとき
P=kx+cx'
の力を受けます。力はx正の向きが正です。
ここで外力F=F_0cos \omega tが作用しているときの運動は自由振動が減衰した後は
x=Xとなるので
\begin{align*}
X&=\frac{\frac{F_0}{k}}{\sqrt{(1-\nu^2)^2+(2\zeta\nu)^2}}cos(\omega t-\phi)\\
X'&=-\frac{\frac{F_0}{k}\omega}{\sqrt{(1-\nu^2)^2+(2\zeta\nu)^2}}sin(\omega t-\phi)
\end{align*}
をそれぞれ代入して
\begin{align*}
P&=\frac{F_0}{\sqrt{(1-\nu^2)^2+(2\zeta\nu)^2}}(cos (\omega t -\phi)-\frac{c\omega}{k}sin(\omega t - \phi))\\
&=\frac{F_0}{\sqrt{(1-\nu^2)^2+(2\zeta\nu)^2}}(cos (\omega t -\phi)
-\frac{2c\omega\times\sqrt{m}}{2\sqrt{mk}\times\sqrt{k}}sin(\omega t - \phi))\\
&=\frac{F_0}{\sqrt{(1-\nu^2)^2+(2\zeta\nu)^2}}(cos (\omega t -\phi)
-2\zeta \nu sin(\omega t - \phi))\\
&=\frac{F_0\sqrt{1+(2\zeta \nu)^2}}{\sqrt{(1-\nu^2)^2+(2\zeta\nu)^2}}cos (\omega t -\phi ^{*})\\
&=P_0cos (\omega t -\phi ^{*})\\
&~~~~~P_0=\frac{F_0\sqrt{1+(2\zeta \nu)^2}}{\sqrt{(1-\nu^2)^2+(2\zeta\nu)^2}}\\
&~~~~~\phi^{*}=\phi+\phi_2,~\phi_2=tan^{-1}(-2\zeta \nu)
\end{align*}となります。
今回位相については複雑になっているので省略します。
伝達率\gammaは以下の様に、外力の振幅F_0と
得られた壁に伝達する力の振幅P_0の比を取ったものです。
\begin{equation}
\gamma=\frac{P_0}{F_0}=\frac{\sqrt{1+(2\zeta \nu)^2}}{\sqrt{(1-\nu^2)^2+(2\zeta\nu)^2}}
\end{equation}こちらを振幅倍率と同様にグラフにしてみます。
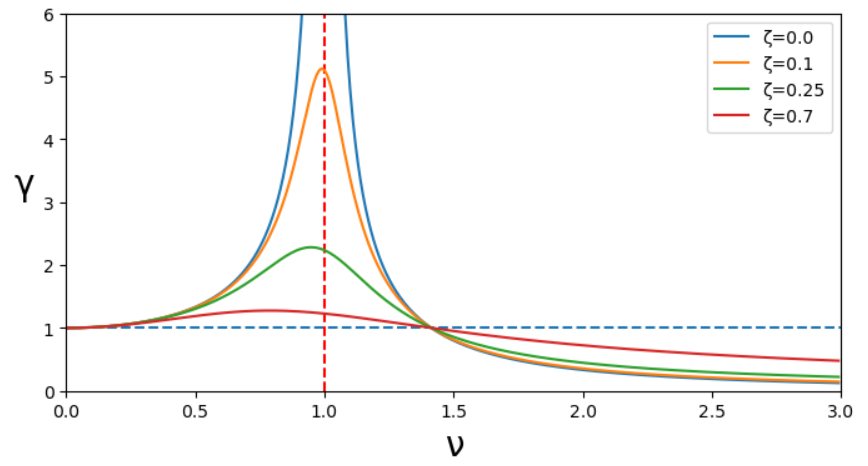

比較のため振幅倍率のグラフも載せています。左が伝達率です。
振幅倍率と似たようなグラフになりましたが、\nuが大きいときの挙動に特徴がみられます。
(分かりにくかったので\zetaがかなり大きい場合を載せています。)
減衰比が大きくなると、\nu=1の共振周波数付近では振幅が小さくなりますが、
その後の振幅の下がり方が悪くなっていることが分かります。
このことから振動を伝達させたくない場合には、\nu<\sqrt{2}で使用し
減衰比\zetaを大きくするか、\nu>\sqrt{2}で減衰を
あまり大きくしないようにするのが良いということになります。
実際にはできれば共振周波数から十分離したいので\nu<\sqrt{2}のときは
\nu<<1にしたいです。
また、\nu>\sqrt{2}で使用する場合には一時的に加速中に共振周波数を
通過することになるので、そこにも注意が必要です。
(減衰が小さすぎる場合や、加速が遅い場合などには振幅が大きくなりすぎて機械が
破損する場合があります。)
\nu<\sqrt{2}の場合、伝達率は1未満にはならないので、
防振ゴムなどの制振材は\nu>\sqrt{2}で使用する場合が多いです。
(ゴムなので柔らかく、共振周波数も低めです。)
防振材のメーカーで防振ゴムなどの、ばねと減衰が一体化した防振材の選定をお願いすると
まず勧められるのが耐荷重を満足するものの中で耐荷重が小さいダンパーだと思います。
これは耐荷重が小さい=ばね定数が小さい=\nuが小さくなるためです。
(使用する回転数が一定の場合)
このときばね定数が小さくなると\zetaが大きくなり、伝達率の下がりが悪くなりますが、
グラフを見てわかる通り、\zetaの変化に対して性能が極端に悪くなるわけではないです。
むしろこれを気にしてばね定数を大きめにしてしまうと、\nuが大さくなり、
逆に伝達率が上がる場合が考えられます。
(\nu>\sqrt{2}であっても\nuが十分大きくないと伝達率が
下がっていかないのはグラフを見ればすぐに分かります。)
今回は物体が壁に与える力を考えましたが、逆に壁が振動し、
ばね・減衰器を介して物体が力を受ける場合も考えられます。
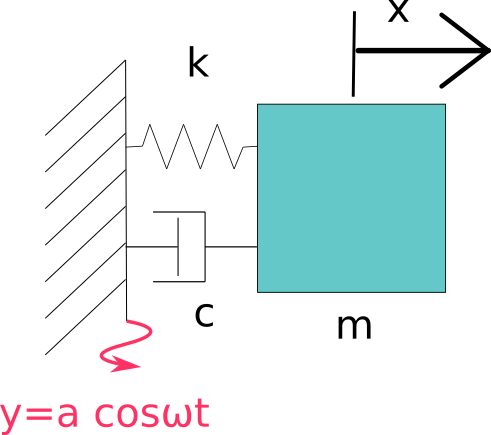
例えば上の図の様に壁がyで振動運動し、その運動によりばね・減衰器を介して
物体が力を受けます。
(通常上図のような書き方をした壁は動かないという意味ですが、
今回はご勘弁ください。)
このような系に対してx_0/aを考えると、その値は\gammaと一致します。
(こちらはそろそろ内容がくどくなってきたのでおまけにつけておきます。
興味のある方だけ見てみてください。)
つまり伝達率は、物体が振動したときの他の物体(壁)への振動伝達のしやすさであり、
逆にほかの物体(壁)が振動しているときの物体への振動伝達のしやすさでもあります。
このように、機械は別の物体から振動を伝達されて振動する場合が多いので、
実際に機械を扱っていると、振幅倍率よりも伝達率を使う機会が多いと思います。
現場等では減衰が大きいほど共振周波数より上での振幅が大きい!と
覚えている方も多いのではないかと思いますが、それは振幅倍率には当てはまりません。
振幅倍率と伝達率は良く似ているので意外とこの辺りを
明確に区別できている人は少ないと思います。
(多分区別していなくてもそこまで困りません。)
ただし、回転機械などの自身が振動の発生源となる機械を扱う場合には
振幅倍率もとても重要です。
(こちらはもう少し違った形で使われる場合が多いと思いますが、ここでは説明しません。)
結言
さて、長くなりましたが、ここまで1自由度の振動系に振動的な外力をかけたときに
どのような運動となるかを見てきました。
得られた結果から、運動は加えられる振動的な外力の周波数により大きく変化することが分かり、
系により振幅が極端に大きくなる共振現象を起こす特定の周波数(共振周波数)を
持つことが分かりました。
これらの変化の様子を周波数に対する関数として示した周波数応答関数は
振動分野を扱う方たちにとっては基本中の基本となるものです。
こちらを理解していただければあなたも一人前の振動屋さんかもしれません。
もちろん振動の分野も奥が深く、これらの発展として様々な問題を取り扱い、
それぞれに特有の現象等があるため、覚えることはまだまだあります。
次回からは本題である回転機械特有の振動について説明していきたいと思います。
また、実際に振動を扱う際に実験から周波数応答や減衰比を求める方法などについても
簡単に説明できたらと思いますので、そのうち番外編でやろうかと思います。
おまけ1:三角関数の式変形について
以下の変形について説明しておきます。
\begin{align*}
X&=\frac{-m\omega ^2 + k}{(-m\omega ^2+k)^2+c^2\omega ^2}F_0cos\omega t+
\frac{c\omega}{(-m\omega ^2+k)^2+c^2\omega ^2}F_0 sin\omega t\\
&=Bcos\omega t +Csin\omega t\\~~\\
X&=\sqrt{B^2+C^2}cos(\omega t-\phi)\\
&=\frac{F_0}{\sqrt{(-m\omega ^2+k)^2+c^2\omega ^2}}cos(\omega t-\phi)\\
&~~\phi = tan^{-1}(\frac{C}{B})=tan^{-1}(\frac{c\omega}{-m\omega ^2+k})
\end{align*}これは三角関数の加法定理の中のcosに関する公式
cos(\alpha-\beta)=cos\alpha cos\beta+sin\alpha sin\beta
より
\begin{align}
cos\beta &= \frac{B}{\sqrt{B^2+C^2}}\\
sin\beta &=\frac{C}{\sqrt{B^2+C^2}}\\
\end{align} とすれば得られます。cos^2\beta + sin^2 \beta = 1でなければならないので\sqrt{B^2+C^2}で割り、
その分が大きさとして式の前方に現れています。
また、これらを満たす\beta=tan^-1(C/B)となります。
厳密には-\pi \leq\beta< \piにおいてtan^-1\betaは2つの値を持ちますが、
C=\frac{c\omega}{(-m\omega ^2+k)^2+c^2\omega ^2}F_0\\より、通常C\geq0であることを考えれば0 \leq\beta \leq \piとなり、一意に決まります。
正確には式(6)(7)を満たす\betaが正解だと思いますが、多くの教科書で
このような記載となっています。
今後特殊な例としてc,\omegaが負となる場合などを扱われる場合もあるかもしれませんので、
この辺りは頭の片隅に置いておきましょう。
(実用上、位相\phiの実際の値について議論する場面は少ないかもしれませんが・・・)
おまけ2:振動する壁から物体が受ける力(運動)

図の様に、ある物体が壁にばねと減衰器でつながっており、
壁が変位y=a~cos \omega tで振動している場合を考えます。
このとき物体がばねから受ける力は
F=-k(x-y)
となります。同様に物体が減衰器から受ける力も
F=-c(x'-y')
となります。
物体にかかる外力は他にないので、運動方程式は
mx''+c(x'-y')+k(x-y)=0
となります。更にyは
\begin{align*}
y&=acos\omega t\\
y'&=-a\omega sin \omega t
\end{align*}
なので
\begin{align*}
mx''+cx'+kx&=cy'+ky=-ca\omega sin \omega t+ka cos \omega t
\end{align*}となります。
これは線形非同次微分方程式で、一番左辺はこれまでに何度も登場した式です。
こちらは減衰により時間経過で0に近づくので、特解Xを求めていきます。
特解Xを
X=Bcos\omega t+Csin\omega t
とします。こちらを代入して(Xの微分は記事の前半にも書いてあるので省略ます。)
\begin{align*}
m(-B\omega^2cos \omega t-C\omega ^2 sin \omega t)+c(-B\omega sin \omega t+C\omega cos \omega t)+k(Bcos \omega t+Csin\omega t)&&\\=-ca\omega sin \omega t+ka cos \omega t\\
(-mB\omega ^2+cC\omega +kB)cos \omega t+(-mC\omega ^2 -cB\omega+kC)sin\omega t
=-ca\omega sin \omega t+ka cos \omega t\\
\end{align*}係数を比較して
\begin{align*}
-mB\omega ^2+cC\omega +kB &=ka\\
-mC\omega ^2 -cB\omega+kC &=-ca\omega
\end{align*}これを計算していきます。
\begin{align*}
B=\frac{k-m\omega^2}{c\omega}C+a\\
\frac{(k-m\omega^2)^2}{c\omega}C +(k-m\omega ^2)a+c\omega C&=ka\\
\frac{(k-m\omega^2)^2+c^2 \omega ^2}{c\omega}C &=ma\omega ^2\\
C&=\frac{mca\omega ^3}{(k-m\omega^2)^2+c^2 \omega ^2}\\
B&=\frac{ma\omega ^2(k-m\omega ^2)}{(k-m\omega^2)^2+c^2 \omega ^2}
+\frac{(k-m\omega^2)^2+c^2 \omega ^2}{(k-m\omega^2)^2+c^2 \omega ^2}a\\
&=\frac{(k-m\omega^2)(m\omega ^2+k-m\omega^2)+c^2\omega ^2}{(k-m\omega^2)^2+c^2 \omega ^2}a\\
&=\frac{k(k-m\omega^2)+c^2\omega ^2}{(k-m\omega^2)^2+c^2 \omega ^2}a\\
\end{align*}更に整理して
\begin{align*}
B&=\frac{(1-\frac{m\omega^2}{k})+\frac{c^2\omega ^2}{k^2}}{(1-\frac{m\omega^2}{k})^2+\frac{c^2 \omega ^2}{k^2}}a\\
&=\frac{(1-\frac{m}{k}\omega^2)+\frac{4c^2m}{4mk\times k}\omega ^2}{(1-\frac{m}{k}\omega^2)^2+\frac{4c^2m}{4mk\times k}\omega ^2}a\\
&=\frac{(1-\nu^2)+(2\zeta \nu)^2}{(1-\nu ^2)^2+(2\zeta \nu)^2}a\\~~\\
C&=\frac{\frac{m}{k}\omega^2\frac{c}{k}\omega }{(1-\frac{m\omega^2}{k})^2+\frac{c^2 \omega ^2}{k^2}}a\\
&=\frac{\nu^2\times2\zeta\nu}{(1-\nu^2)^2+(2\zeta\nu)^2}a
\end{align*}これらをもとのXに代入して
\begin{align*}
X&=\frac{(1-\nu^2)+(2\zeta \nu)^2}{(1-\nu ^2)^2+(2\zeta \nu)^2}acos\omega t
+\frac{\nu^2\times2\zeta\nu}{(1-\nu^2)^2+(2\zeta\nu)^2}asin \omega t\\
&=\frac{\sqrt{(1-\nu^2)^2+2(1-\nu ^2)(2\zeta\nu)^2+(2\zeta \nu)^4 +
\nu ^4(2\zeta\nu)^2}}{(1-\nu ^2)^2+(2\zeta \nu)^2}acos(\omega t -\phi)\\
&=\frac{\sqrt{(1-\nu^2)^2+\{2-2\nu ^2+\nu ^4\}(2\zeta\nu)^2+(2\zeta \nu)^4 }}{(1-\nu ^2)^2+(2\zeta \nu)^2}acos(\omega t -\phi) \\
&=\frac{\sqrt{(1-\nu^2)^2+\{(1-\nu^2)^2+1\}(2\zeta\nu)^2+(2\zeta \nu)^4 }}{(1-\nu ^2)^2+(2\zeta \nu)^2}acos(\omega t -\phi) \\
&=\frac{\sqrt{(1-\nu^2)^2\{(2\zeta\nu)^2+1 \}+(2\zeta\nu)^2\{1+(2\zeta \nu)^2\} }}{(1-\nu ^2)^2+(2\zeta \nu)^2}acos(\omega t -\phi) \\
&=\frac{\sqrt{\{(1-\nu^2)^2+(2\zeta\nu)^2 \}\{1+(2\zeta \nu)^2\} }}{(1-\nu ^2)^2+(2\zeta \nu)^2}acos(\omega t -\phi) \\
&=\frac{\sqrt{1+(2\zeta \nu)^2 }}{\sqrt{(1-\nu ^2)^2+(2\zeta \nu)^2}}acos(\omega t -\phi) \\
&=x_0cos(\omega t - \phi)\\
&~~\phi=tan^{-1}\frac{\nu^2\times2\zeta\nu}{(1-\nu^2)+(2\zeta \nu)^2}
\end{align*}
このx_0をaで割って
\gamma '=\frac{x_0}{a}=\frac{\sqrt{1+(2\zeta \nu)^2 }}{\sqrt{(1-\nu ^2)^2+(2\zeta \nu)^2}}となり、壁から物体への伝達率\gamma 'が得られました。これは式(5)と一致しています。
このことから、伝達率はお互いへの振動の伝達しやすさを表していることが分かります。
最後に、位相\phiについてグラフを載せておきます。
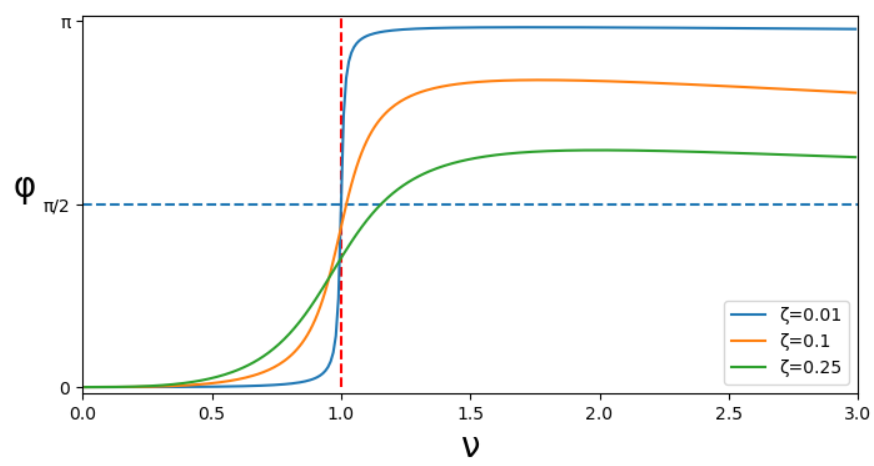
それほど大きくない減衰比であっても\phi=\piに到達しなさそうであったり、
\nu=1で\phi=\pi/2を通らないなど、
通常見られる位相の曲線と少し様子が異なります。
記事の中で共振時の位相は\phi=\pi/2となると言いましたが、
伝達率を見る場合にはその限りではないようです。
自分が測定しているものが伝達率なのか、振幅倍率なのか、
またはほかの周波数応答関数なのかを理解して、
このような位相を総合的に判断できるようになるとよいと思います。