前回の記事では不減衰自由振動について説明しました。
(前回の記事はこちら)
減衰のない振動系に力が加わっていない場合、初期の位置や速度により振動運動をします。
このような振動運動では、振動系の持つ特性(質量m、ばね定数k)により特定の周波数で、
一定の振幅を保ち運動し続けますが、現実では一度動き出した物体が永久に運動し続ける
ということはほぼあり得ません。
このような違いが表れる理由が減衰です。
現実に存在するほとんどのものは、大なり小なり減衰を持っています。
この減衰により、振動エネルギーが熱エネルギーへと変換され、振動運動は収まっていきます。
減衰振動
減衰とは
まず減衰について説明したいと思います。
上にも書いた通り、減衰とは運動エネルギーを熱エネルギー等に不可逆的に変換するものです。
(減衰については手持ちの教科書等には正確な定義がなく、私なりの解釈になります。)
そのなかでも、高校でも学び、最もありふれた減衰は摩擦減衰だと思います。
摩擦力は以下の式で表されます。

\begin{align*}
F_f&=-F_~~&(F \leq F'のとき )\\
F_f&=\mu 'N~~(ただし速度と逆方向)&(F>F'のとき)\\\\
&F_f :摩擦力\\
&F:外力(摩擦面に平行)\\
&F'=\mu N:最大静止摩擦力\\
&\mu :静止摩擦係数\\
&\mu ':動摩擦係数\\
&N:垂直抗力
\end{align*}少しごちゃごちゃしていますが、高校までの物理でも学習していると思います。
(記憶が曖昧ですが、小学校とかでも習ったような気がします。)
一般に\mu > \mu'なので、外力Fに対する摩擦力f_fは
下記の様なグラフになります。
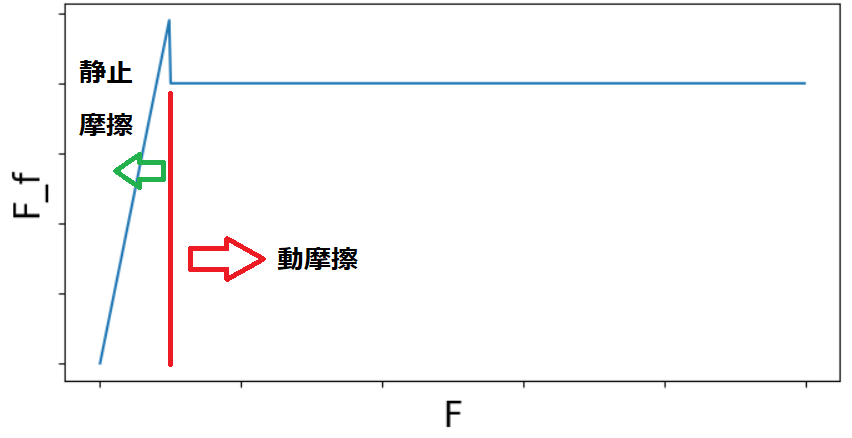
長々と説明しましたが、このような摩擦力による摩擦減衰は非線形(単純な直線ではない)ので、
これまで扱ってきたような線形の微分方程式では扱うことが難しいです。
そこで一般的な振動問題では、減衰として粘性減衰を用います。
粘性減衰
粘性減衰はその名の通り、粘性のある物体(液体など)による減衰を式としてモデル化したものです。
粘性減衰による減衰力F_cは以下の様に表されます。
\begin{equation}F_c=-cv=-cx' ~~~~~~ c:粘性減衰係数\end{equation}粘性減衰力は物体の速度vに比例し、その方向は速度の逆向きです。
粘性減衰係数cは通常正の数となります。
モデル上で粘性減衰を表す場合、下記の様な記号を使用する場合が多いです。

記号としてはダッシュポッドを簡略化したような形状です。
この図では左側の固定された壁と、右側の緑色の物体の間に粘性減衰があることを表しています。
粘性減衰は元々はダッシュポッドの様な粘性流体等を利用した減衰のモデル化ですが、
ゴムダンパなど、減衰として使用される物体の減衰もある程度近似できるようなので、
計算上の扱いが良いこともあって振動の分野ではよく使われます。
ただし、これはあくまで近似であり、現実では完全にこの式の通りの減衰力が働くわけではありません。
例えば同じモデルでも速度が大きく変わる場合には減衰係数が一定ではないこともあり得ますし、
振動の周波数により減衰が変化する場合もあります。
これはモデルの元となった粘性流体を用いた減衰であっても同じです。
あくまで扱いやすいように定式化したものであることを忘れないようにしてください。
減衰自由振動
振動分野で扱う最も単純な減衰ありの振動系は、以下の様なものになります。

減衰なしのモデルに減衰cが追加されたものです。
一応説明すると、質量mの物体が左側の壁に対し、ばね定数kのばねと、粘性減衰係数cの減衰器でつながっており、
物体は左右方向xに運動します。
ばねがないと振動運動をしないので減衰器のみのモデルは扱いません。
現実的には、ばねも多少の減衰を持ち、減衰器も何らかのばね性を持っているので、
どちらかのみのモデルというのはほぼ存在しません。
(ただし、金属製のばねなどの減衰はかなり小さく、
単純な近似として減衰なしモデルを使用する場合はあります。)
このようなモデルに対し、外力が働かない場合を考えます。
減衰ありのモデルで外力のない自由振動ですので、減衰自由振動と呼ばれます。
減衰自由振動の運動方程式
減衰自由振動の運動方程式は以下の様になります。
mx''=F=-kx-cx'
さらに整理すると
\begin{align}
mx''+cx'+kx = 0
\end{align}となり、線形同次微分方程式となります。
線形同次微分方程式の解法は以前の記事で説明していますので、そちらを参照してください。
回転機械の振動 番外編1. 微分方程式の解法
では解法通り解いていきます。まずは特性方程式を得ます。x = e^{\lambda t}を代入し、
m\lambda^2 +c\lambda+k = 0
これを解くと、2次方程式の解の公式から
\lambda = \frac{-c\pm \sqrt{c^2-4mk}}{2m}さらに扱いやすいように整理して
\begin{align*}
\lambda &= -\frac{c}{2m}\pm \sqrt{\frac{c^2}{4m^2}-\frac{4mk}{4m^2}}\\
&= -\frac{c}{2m}\pm \sqrt{\frac{c^2}{4m^2}-\frac{k}{m}}\\
&= -\frac{c}{2m}\pm \sqrt{(\frac{c}{2m})^2-(\sqrt{\frac{k}{m}})^2}
\end{align*}となります。最後の行は振動運動を解析していく上で便利な形にするための変形です。
これを解法の一般解に代入すると
\begin{align}
x&=C_{1}e^{(-\frac{c}{2m}+ \sqrt{(\frac{c}{2m})^2-(\sqrt{\frac{k}{m}})^2})t}
+C_{2}e^{(-\frac{c}{2m}- \sqrt{(\frac{c}{2m})^2-(\sqrt{\frac{k}{m}})^2})t}
~~~ (C_1,C_2は定数)
\end{align}となります。
とても複雑な式となっており、すぐにはどのような運動を表しているのか分かりません。
さらに詳しく見ていきましょう。
減衰自由振動の種類
不減衰自由振動ではeの乗数が虚数であったため振動運動となりましたが、
今回はeの乗数が複雑であり、実数の場合と虚数(複素数)の場合があります。
実はこれらの場合により(3)式の表す運動が異なります。
まずはeの乗数が実数となる場合を見ていきましょう。
eの乗数が実数の場合
eの乗数は (-\frac{c}{2m}\pm \sqrt{(\frac{c}{2m})^2-(\sqrt{\frac{k}{m}})^2})t なので、
これが実数となるのは平方根の中身が正の場合で
(\frac{c}{2m})^2-(\sqrt{\frac{k}{m}})^2>0のときとなります。この式をcについて考えてみると(m,kはすべて正なので)
\begin{align*}
\frac{c^2}{4m^2}&> \frac{k}{m}\\
c^2&>4mk\\
c<-2\sqrt{mk}, &2\sqrt{mk} < c
\end{align*}cも通常扱う場合では正なので、2\sqrt{mk} < cが条件となります。
この条件が切り替わる2\sqrt{mk}を臨界粘性減衰係数c_cと呼びます。
臨界粘性減衰係数 c_c=2\sqrt{mk}
さて、実際に運動を調べてみます。
eの乗数の中身を見ていくとそれぞれの項は
\begin{align}
(-\frac{c}{2m}+ \sqrt{(\frac{c}{2m})^2-(\sqrt{\frac{k}{m}})^2})t\\
(-\frac{c}{2m}- \sqrt{(\frac{c}{2m})^2-(\sqrt{\frac{k}{m}})^2})t\\
\end{align}となりますが、このうち(5)式は平方根内が正の実数なので-Bt (B>0:定数)と表せることが
すぐにわかります。
一方で(4)の式ですが、m,c,kが正であり平方根内が正の実数なので
\frac{c}{2m}> \sqrt{(\frac{c}{2m})^2-(\sqrt{\frac{k}{m}})^2}ということが分かります。
つまりこちらも-At (A>0:定数)と表すことができます。
y=e^{-ax} (a>0)が0に漸近することは高校数学等でも学習すると思いますが、
一応グラフを載せておきます。
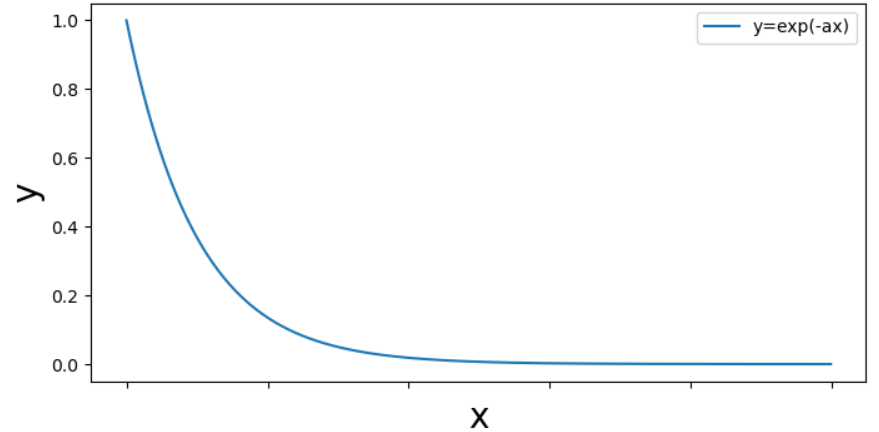
eの乗数が実数の場合の運動はこのような0に漸近する項の線形和で表されるので、
その運動も似たような曲線を描いて0に近づいていきます。
まとめると、減衰係数cが臨界粘性減衰係数c_cよりも大きいとき、
減衰自由振動系は振動せずに振幅が0へと近づいていきます。
ただし、ここで減衰係数c=c_cからcが大きくなるほど、
実は振幅が0になるまでの時間が長くなります。
このことから、c>c_cとなる減衰を過減衰、
c=c_cとなる減衰を臨界減衰と呼びます。
厳密にはc=c_cとなる場合の運動の説明をしていませんが、
こちらは記事末尾におまけとして記載しておきます。
また、減衰が大きくなるほど振幅が0になるまでの時間が長くなる数学的説明も
末尾に記載しておきます。
eの乗数が虚数(複素数)の場合
eの乗数が虚数となるのは、上の場合とは反対に平方根の中身が負の場合なので、同様に
\begin{align*}
(\frac{c}{2m})^2-(\sqrt{\frac{k}{m}})^2 &<0\\
\frac{c^2}{4m^2}&< \frac{k}{m}\\
c^2&<4mk\\
-2\sqrt{mk}< c&<2\sqrt{mk}
\end{align*}cを正とすると
0< c<2\sqrt{mk} =c_c
という条件になります。このときの運動はλが以下の様に表せるので
\lambda = -\frac{c}{2m}\pm i\sqrt{-(\frac{c}{2m})^2+(\sqrt{\frac{k}{m}})^2}これをx=e^{\lambda t}に代入して
\begin{align*}
x&=C_{1}e^{(-\frac{c}{2m}+ i\sqrt{-(\frac{c}{2m})^2+(\sqrt{\frac{k}{m}})^2})t}
+C_{2}e^{(-\frac{c}{2m}- i\sqrt{-(\frac{c}{2m})^2+(\sqrt{\frac{k}{m}})^2})t}
~~~ (C_1,C_2は定数)
\\
&=C_{1}e^{-\frac{c}{2m}t}×e^ {i\sqrt{-(\frac{c}{2m})^2+(\sqrt{\frac{k}{m}})^2}t}
+C_{2}e^{-\frac{c}{2m}t}×e^ {-i\sqrt{-(\frac{c}{2m})^2+(\sqrt{\frac{k}{m}})^2}t} \\
&=e^{-\frac{c}{2m}t}(C_{1}e^ {i\sqrt{-(\frac{c}{2m})^2+(\sqrt{\frac{k}{m}})^2}t}
+C_{2}e^ {-i\sqrt{-(\frac{c}{2m})^2+(\sqrt{\frac{k}{m}})^2}t}) \\
&=e^{-\frac{c}{2m}t}\{A^{*}cos\sqrt{-(\frac{c}{2m})^2+(\sqrt{\frac{k}{m}})^2}t
+B^{*}sin{\sqrt{-(\frac{c}{2m})^2+(\sqrt{\frac{k}{m}})^2}t} \} \\
&=Ae^{-\frac{c}{2m}t}cos(\sqrt{-(\frac{c}{2m})^2+(\sqrt{\frac{k}{m}})^2}t -\phi)
\end{align*}となります。オイラーの公式を用いた変形は前回の記事を参考にしてください。
回転機械の振動 2-1.振動の基本-不減衰自由振動
ここで得られた式をさらに細かく見てみます。
cosの部分が振動運動を表していることは前回の記事で示した通りですが、
今回は振幅を表していたAの項にe^{-\frac{c}{2m}t}が掛けられています。
c,mが正なので、-\frac{c}{2m}は負となり、e^{-\frac{c}{2m}t}は上で示したような
時間とともに0に漸近するような曲線を描きます。
これにより物体は振動運動をしながら、その振幅は時間とともに0に漸近するような
運動となります。
実際にグラフにしたものがこちらになります。(A=1、\phi = 0)
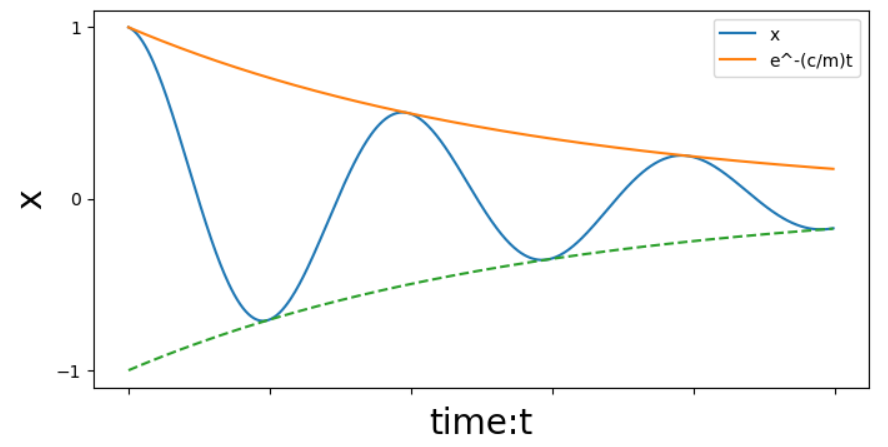
青で示される振動運動が実際の運動になります。
参考としてcosの左側に掛けられている振幅に相当する部分e^{-\frac{c}{2m}t}と、
それをx=0について反転したグラフを載せています。
振動運動が減衰され、時間が経つにつれて0に近づいていくのが分かると思います。
これは現実世界で、ばねのついた物体を引っ張り、静かに離したときの
振動運動のイメージに近いのではないかと思います。
eの乗数に現れる係数-\frac{c}{2m}はcが大きいほど(負なので)小さくなり、
e^{-\frac{c}{2m}t}はより早く0に近づくことになるため、
物体が減衰振動をする範囲では粘性減衰係数cが大きいほど早く減衰することになります。
減衰自由振動のまとめ
これまでの説明をまとめると、減衰自由振動は以下の様に場合分けされます。
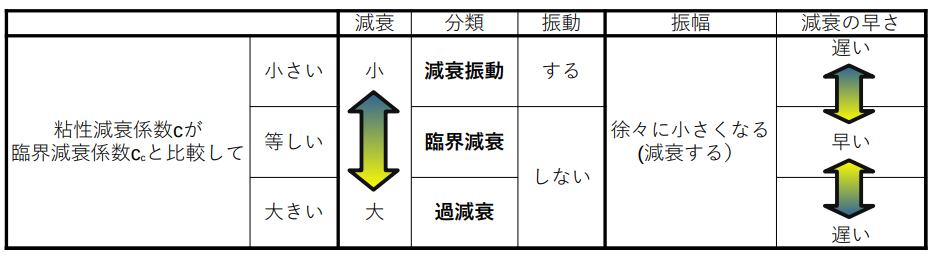
振幅の減衰は、臨界減衰の点で早遅が入れ替わります。
なんとなく臨界減衰や過減衰という名称の意味が分かるのではないかと思います。
振動問題を扱う際に用いられるパラメータ
ここからは振動問題を扱う際によく用いられるパラメータ(物理量)について説明します。
これまでの説明から、粘性減衰係数cは臨界粘性減衰係数c_cに比べて大きいかどうかが
振動を扱う際には重要であることが分かったと思います。
そこで粘性減衰係数cと臨界粘性減衰係数c_cの比をとったパラメータとして
減衰比 ~\zeta=\frac{c}{c_c}=\frac{c}{2\sqrt{mk}}減衰比 \zeta=\frac{c}{c_c}=\frac{c}{2\sqrt{mk}}
が用いられます。
これまでの説明から0 < \zeta < 1では減衰振動運動となり、
\zeta \geq 1では振動のない減衰運動となります。
また、不減衰自由振動の振動周波数を
不減衰固有振動数 \omega _n=\sqrt{\frac{k}{m}}
と呼びます。これは外力がない場合に、その物体が勝手にその振動数(周波数)で振動する
固有の振動数という意味です。
さて、これらの減衰比と不減衰固有振動数を用いると、eの乗数に現れた複雑な項(4)(5)を
以下の様に書き表すことができます。
\begin{align*}
\frac{c}{2m}&=\frac{c\sqrt{k}}{2m\sqrt{k}}=\frac{c\sqrt{k}}{2\sqrt{mk} ×\sqrt{m}}=\frac{c}{c_c}×\sqrt{\frac{k}{m}}=\zeta \omega _n~より\\
式(4)(5) &=(-\frac{c}{2m}\pm \sqrt{(\frac{c}{2m})^2-(\sqrt{\frac{k}{m}})^2})t\\
&=(-\zeta \omega _n \pm \sqrt{(\zeta \omega _n )^2- \omega _n^2})t\\
&=(-\zeta \omega _n \pm \omega _n\sqrt{\zeta^2- 1})t\\
&=(-\zeta \pm\sqrt{\zeta^2- 1})\omega _n t\\
\end{align*}これにより、これまでごちゃごちゃと減衰自由振動について説明してきましたが、
減衰自由振動はm,c,kから計算される2つのパラメータのみで特性を表せることが分かりました。
これにより特に振動運動となる場合のxは
x=Ae^{-\zeta \omega _n t}cos(\sqrt{1-\zeta ^2}\omega _nt-\phi)と表現できます。このことから減衰振動時の振動周波数\omega_dは
減衰固有振動数 \omega_d=\omega _n \sqrt{1-\zeta ^2}
と表されることもわかります。
減衰振動となる場合には\zeta < 1なので、固有振動数が不減衰固有振動数に比べて
低くなることが分かります。
ただし現実的に機械で扱われる振動系では減衰はそこまで大きくなく、
\omega _n \approx \omega _dとなる場合がほとんどです。
(なので固有振動数=\sqrt{k/m}とだけ覚える人が多いです。)
また、それ以外に減衰を表す指標として
対数減衰率 \delta=\frac{2\pi\zeta}{\sqrt{1-\zeta^2}}
というパラメータが用いられる場合もあります。このパラメータは減衰が小さい場合には
\delta \approx 2\pi \zeta
となり、実用上で扱うような振動問題では上式が用いられます。
このパラメータは減衰振動波形から減衰比の値を得るために用いられるものですが、
今回はその説明はしません。
今後説明する場合には再度説明するので覚えなくても問題ありません。
結言
以上が減衰自由振動の説明になります。
次回以降はこれまで説明してきた振動系に外力が掛かるような強制振動と、
それにより得られる振動系の特性について説明していきたいと思います。
おまけ1:臨界減衰の運動(c=c_cのとき)
c=c_cとなるときの運動は単純に式(3)平方根内を0として
\begin{align}
x&=C_{1}e^{-\frac{c}{2m}t}
+C_{2}e^{-\frac{c}{2m}t}
~~~ (C_1,C_2は定数)
\end{align}と考えても、物理的にはそこまで問題はありません。
しかし、上式を見てわかる通り、C1,C2に掛けられている項が共通になっており、
独立性が確保されていません。
これでは線形微分方程式の一般解としては不十分です。
c=c_cとなるのは線形同次微分方程式の解法を説明した以前の記事の、
おまけで説明している重解を持つ場合にあたります。
このときの線形微分方程式の一般解は
x = C_1te^{\lambda _1 t}+C_2e^{\lambda _1 t}~~~~~(\lambda _1 = -\frac{c}{2m}=-\zeta \omega_n = -\omega_n)となります。
2項目のe^{\lambda _1 t}が0に漸近することは既知ですので、
1項目のte^{\lambda _1 t}について調べてみます。
\begin{align*}
X&=te^{\lambda _1 t}\\
&=\frac{t}{e^{-\lambda _1 t}}\\
\lim _{t \to \infty}X&=0~~~(\because logx \lll x^a \lll a^x ~~x \to \infty)
\end{align*}
調べてみたところ、logx \lll x^a \lll a^xは高校数学でも常識と言ってよいようなので
そのまま流用しました。一応ロピタルの定理を用いた証明をさらに末尾に付録しておきます。
また、Xを微分すると
\begin{align*}
X'&=e^{\lambda _1 t}+\lambda _1 te^{\lambda _1 t}\\
&=(\lambda_1t+1)e^{\lambda_1 t}
\end{align*}\lambda _1 =-\omega _n < 0なので、Xの微分X’はt =-1/\lambda _1まで正で、
それ以降は負となります。
これらを総合すると、te^{\lambda _1 t}はt=-1/\omega _nまでは振幅が大きくなり、
その後は振幅が小さくなって0に漸近します。
実際にグラフで表すと以下の様になります。

減衰して振幅が小さくなると言いながら、なぜ振幅が大きくなっているのかと思う方もいるかもしれません。
これは初期条件によるもので、例えば振幅1mmのところから位置0の方向に
時速100kmで物体を離したとしましょう。
(こんなことは実際には難しいと思いますが、理論上はありえます。)
いくら減衰があるとは言え、これを1mm進む間に減衰して速度0にすることはできず、
どう考えても位置0のラインを越えて逆側に向かってしまうはずです。
これまで扱ってきた式は一般解なので、このような条件の運動もすべて含んでいます。
初期条件が速度なしで静かに離すという場合にはこの項の定数係数C_1=0となり、
このような振幅が増える運動にはなりません。
説明しませんでしたが、実はこのような一時的に振幅が増える運動は
過減衰の場合も起こりえます。
過減衰運動の項であるe^{-At}はそれぞれ時間とともに0に近づいていきますが、
その定数係数C_1,C_2の符号が異なる場合には同様の運動となる場合があります。
この場合も最終的には振動せずに振幅が0に近づいていきます。
おまけ2:過減衰運動時の減衰の早さについて
過減衰運動時に、減衰が大きくなるほど振幅が0になるまでの時間が長くなることについても説明しておきます。
この辺りについて説明している教科書が見当たらなかったので、
少々強引な説明になってしまいますが温かい目で見てください。
まずは初期条件としてt=0でx=A>0、x’=0とします。
これは上のおまけ1でも説明した通り、初期条件により特殊な運動となる場合があり、
これらすべてを一括で処理するには私の数学力が不足しているためです。
ただしこのようなx’=0の条件を満たす時間t、振幅Aは(t<0、A<0を含まれば)
初期条件を変えても通常存在します。
その時間を新たにt=0とすれば今回説明する運動と同様の運動になります。
まずはC_1 、C_2を求めます。
\begin{align}
x&=C_1 e^{(-\zeta + \sqrt{\zeta^2-1})\omega_nt}+C_2e^{(-\zeta-\sqrt{\zeta^2-1})\omega _n t}\\
x'&=C_1 \omega _n (-\zeta+\sqrt{\zeta^2-1})e^{(-\zeta +\sqrt{\zeta ^2 -1})\omega _nt}+C_2 \omega_n (-\zeta-\sqrt{\zeta^2-1})e^{(-\zeta-\sqrt{\zeta^2-1})\omega _n t}\\
&=\omega_n e^{-\zeta \omega_n t}\{C_1(-\zeta+\sqrt{\zeta^2-1})e^{\sqrt{\zeta ^2 -1}\omega _nt}+C_2(-\zeta-\sqrt{\zeta^2-1})e^{-\sqrt{\zeta ^2 -1}\omega _nt}\}
\end{align}
ここにt=0、x=A、x’=0を代入します。
C_1+C_2=A\\
C_1 \omega _n (-\zeta+\sqrt{\zeta^2-1})+C_2 \omega_n (-\zeta-\sqrt{\zeta^2-1})=0\\
これを解くと以下の定数が得られます。
\begin{align*}
C_1 &= \frac{\zeta+\sqrt{\zeta^2 -1}}{2\sqrt{\zeta^2 -1}}A\\
C_2 &= \frac{-\zeta+\sqrt{\zeta^2 -1}}{2\sqrt{\zeta^2 -1}}A\\
\end{align*}これを式(7)に代入します。また、記述を簡単にするため
\begin{align*}
e^{+}&=e^{-\zeta \omega_nt+\sqrt{\zeta ^2 -1}\omega _nt}\\
e^{-}&=e^{-\zeta \omega_nt-\sqrt{\zeta ^2 -1}\omega _nt}\\
\end{align*}の表記を使用します。実際に代入していきましょう。
\begin{align*}
x=&\frac{\zeta +\sqrt{\zeta ^2 -1}}{2\sqrt{\zeta^2 -1}}Ae^{-\zeta \omega_nt+\sqrt{\zeta ^2 -1}\omega _nt}
+\frac{-\zeta +\sqrt{\zeta ^2 -1}}{2\sqrt{\zeta^2 -1}}Ae^{-\zeta \omega_n t -\sqrt{\zeta ^2 -1}\omega _nt}\\
=&\frac{\zeta }{2\sqrt{\zeta^2 -1}}A(e^{+}-e^{-})
+\frac{\sqrt{\zeta ^2 -1}}{2\sqrt{\zeta^2 -1}}A(e^{+}+e^{-})\\
=&\frac{\zeta }{2\sqrt{\zeta^2 -1}}A(e^{+}-e^{-})
+\frac{1}{2}A(e^{+}+e^{-})\\
\end{align*}この振幅xが減衰比\zetaに対してどのように変化するかを調べるため、
\zetaについて微分していきます。
(元は減衰cについてなのでcについて微分するのが本来ですが、
式が複雑になり、m,kがある定数であればc \to大で\zeta \to大であるため
\zetaについて調べていきます。)
\begin{align*}
\frac{dx}{d\zeta}=&\frac{2\sqrt{\zeta ^2 -1}-\zeta\frac{2\zeta}{\sqrt{\zeta^2 -1}} }{4(\zeta^2 -1)}A(e^{+}-e^{-})\\
&+\frac{\zeta }{2\sqrt{\zeta^2 -1}}A\{(-\omega_n t+\omega_n t\frac{\zeta}{\sqrt{\zeta^2 -1}})e^{+}
-(-\omega_n t-\omega_n t\frac{\zeta}{\sqrt{\zeta^2 -1}})e^{-}\}\\
&+\frac{1}{2}A\{(-\omega_n t+\omega_n t\frac{\zeta}{\sqrt{\zeta^2 -1}})e^{+}
+(-\omega_n t-\omega_n t\frac{\zeta}{\sqrt{\zeta^2 -1}})e^{-}\}\\~~\\
=&\frac{2(\zeta ^2 -1)-2\zeta^2 }{4(\zeta^2 -1)\sqrt{\zeta^2 -1}}A(e^{+}-e^{-})\\
&+\frac{\zeta \omega_ n t}{2\sqrt{\zeta^2 -1}}A\{\frac{-\sqrt{\zeta ^2 -1}+\zeta}{\sqrt{\zeta^2 -1}}e^{+}
+\frac{\sqrt{\zeta ^2 -1}+\zeta}{\sqrt{\zeta^2 -1}}e^{-}\}\\
&+\frac{\omega_n t}{2}A\{\frac{-\sqrt{\zeta ^2 -1}+\zeta}{\sqrt{\zeta^2 -1}}e^{+}
-\frac{\sqrt{\zeta ^2 -1}+\zeta}{\sqrt{\zeta^2 -1}}e^{-}\}\\~~\\
=&-\frac{1 }{2(\zeta^2 -1)\sqrt{\zeta^2 -1}}A(e^{+}-e^{-})\\
&+\frac{ \omega_ n t}{2(\zeta^2 -1)\sqrt{\zeta^2 -1}}A\{(-\zeta(\zeta ^2 -1)+\zeta^2 \sqrt{\zeta ^ 2 -1}) e^{+}
+(\zeta(\zeta ^2 -1)+\zeta^2 \sqrt{\zeta ^ 2 -1}) e^{-}\}\\
&+\frac{\omega_n t}{2(\zeta^2 -1)\sqrt{\zeta^2 -1}}A\{(\zeta ^2 -1)(-\sqrt{\zeta ^2 -1}+\zeta) e^{+}
-(\zeta ^2 -1)(\sqrt{\zeta ^2 -1}+\zeta) e^{-}\}\\~~\\
=&-\frac{1 }{2(\zeta^2 -1)\sqrt{\zeta^2 -1}}A(e^{+}-e^{-})\\
&+\frac{ \omega_ n t}{2(\zeta^2 -1)\sqrt{\zeta^2 -1}}A\{(-\zeta(\zeta ^2 -1)+\zeta^2 \sqrt{\zeta ^ 2 -1}
-(\zeta ^2 -1)\sqrt{\zeta ^2 -1} +\zeta (\zeta ^2 -1)) e^{+}\\
&~~~~~~~~~~~~~~~~+(\zeta(\zeta ^2 -1)+\zeta^2 \sqrt{\zeta ^ 2 -1}-(\zeta ^2 -1)\sqrt{\zeta ^2 -1}
-\zeta (\zeta ^2 -1)) e^{-}\}\\ ~~\\
=&-\frac{1 }{2(\zeta^2 -1)\sqrt{\zeta^2 -1}}A(e^{+}-e^{-})\\
&+\frac{ \omega_ n t}{2(\zeta^2 -1)\sqrt{\zeta^2 -1}}A\{\sqrt{\zeta ^2 -1} e^{+}+\sqrt{\zeta ^2 -1} e^{-}\}\\~~\\
=&\frac{1}{2(\zeta^2 -1)\sqrt{\zeta^2 -1}}A\{( \omega_ n t\sqrt{\zeta ^2 -1} -1) e^{+}
+( \omega_ n t\sqrt{\zeta ^2 -1} +1)e^{-}\}\\
\end{align*}式が長くなってしまいましたが、最終的な式の形は意外とシンプルになったので、
もっと良い微分の方法があるかもしれません。
得られた式は振幅xの\zetaの変化に対する変化なので、
この式が正であれば、減衰が大きいほど同じ時間での振幅が大きい。
(=減衰が遅い)ということが言えます。
このような視点で最後の式を見てみます。\zeta>1、A>0なので
\begin{equation}
\frac{1}{2(\zeta^2 -1)\sqrt{\zeta^2 -1}}A
\end{equation}の部分は正となります。一方で
\begin{equation}
( \omega_ n t\sqrt{\zeta ^2 -1} -1) e^{+}
+( \omega_ n t\sqrt{\zeta ^2 -1} +1)e^{-}
\end{equation}の部分は\zetaの値次第で(負+正)の形式になっており、
これらの大小関係によって正負が変化します。加えて
\begin{align*}
e^{+}&>e^{-}\\
( \omega_ n t\sqrt{\zeta ^2 -1} -1)&<( \omega_ n t\sqrt{\zeta ^2 -1} +1)
\end{align*}という関係のため大小関係をすぐに判断できなくなってます。
そこで更に式(11)を詳しく見ていきます。式(11)をそのまま微分しても多分良いのですが、
計算が複雑になるのでもう少し整理し、都合がよい形式に変形します。
\begin{align*}
式(11)=&(\omega _n t\sqrt{\zeta ^2 -1} -1) e^{-\zeta \omega _n t+\sqrt{\zeta^2-1}\omega _n t}+
( \omega _n t\sqrt{\zeta ^2 -1} +1)e^{-\zeta \omega _n t-\sqrt{\zeta^2-1}\omega _n t}\\
=&e^{-\zeta \omega _n t-\sqrt{\zeta^2 -1}\omega_n t}(\omega _n t\sqrt{\zeta ^2 -1} +1)(\frac{\omega _n t\sqrt{\zeta ^2 -1} -1}{\omega _n t\sqrt{\zeta ^2 -1} +1}e^{2\sqrt{\zeta^2 -1} \omega_n t}+1)
\end{align*}2項目は正なので、そちらでまとめる形にしました。この式の末尾の項である
\frac{\omega _n t\sqrt{\zeta ^2 -1} -1}{\omega _n t\sqrt{\zeta ^2 -1} +1}e^{2\sqrt{\zeta^2 -1} \omega_n t}+1 =Xが正であることを示せばよいということになります。
ここで\sqrt{\zeta ^2 -1} = yと置き、表記を単純化します。
\zeta \to 大 で y \to 大なので関係性に変化はなく、
\zeta >1 よりy >0 となります。
まずt>0なのでXのt=0のときの値を求めると
\begin{align*}
X&=\frac{\omega _n ty -1}{\omega _n ty +1}e^{2y \omega_n t}+1 \\
X|_{y = 0}&=\frac{-1}{+1}×1+1=0
\end{align*}となります。次にXをyで微分して
\begin{align*}
\frac{dX}{dy}&=\frac{\omega _n t(\omega_n t y +1)-\omega_nt(\omega _n ty -1)}{(\omega _n ty +1)^2}e^{2y\omega _n t}+\frac{\omega _n ty -1}{\omega _n ty +1}×2\omega _n te^{2y\omega _n t}\\
&=\frac{2\omega_n t}{(\omega _n ty +1)^2}e^{2y\omega _n t}+\frac{2 \omega_nt(\omega _n^2 t^2y^2 -1)}{(\omega _n ty +1)^2}× e^{2y\omega _n t}\\
&=\frac{2\omega_n ^3 t^3y^2}{(\omega _n ty +1)^2}e^{2y\omega _n t}>0
\end{align*}となるので、Xは単調増加関数であり、t>0ではX>0ということになります。
これにより\frac{dx}{d\zeta} > 0が言えるので、
減衰cが大きいほど減衰比\zetaが大きく、
減衰比\zetaが大きいほどある時間における振幅xが大きくなります。
つまり振動が収まるまでの時間が長くなるということです。
ちなみにAが負の場合\frac{dx}{d\zeta} < 0となりますが、
これは振幅がマイナス側に大きいという意味ですので、同じ理屈が成り立ちます。
実際に減衰比を変化させたときの振幅をグラフにしてみました。
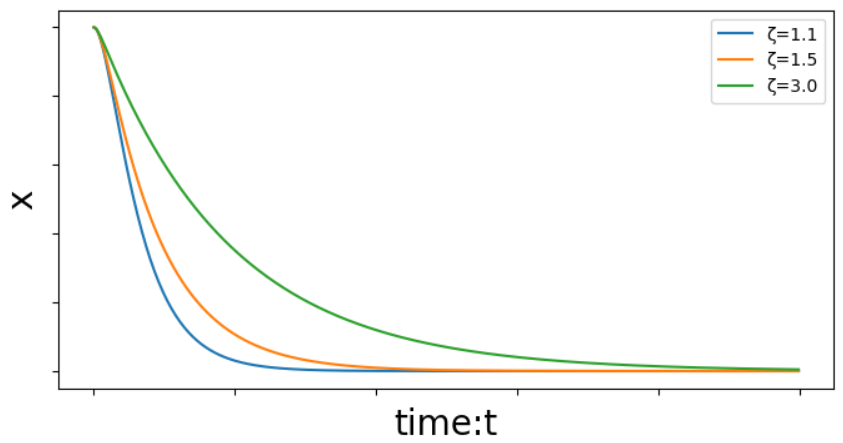
条件は今回求めたt=0でx=A,x’=0となる場合で、k,m等のパラメータは適当に決めています。
正直これまで長々と書いてきましたが、実務上は、
過減衰運動時には減衰が大きいほど振幅の減衰が遅くなる
ということだけ知っていれば大丈夫です。
ただ、この辺りの理由をグラフに描く以上の説明をしている教科書も見当たりませんでしたので、
今回実際に数学的に計算をしてみました。
厳密には初速x’≠0の場合でも成り立つように計算するべきだと思いますが、
今のところそれに関して記述するつもりはありません。
(t=0を変化させることでその他の場合も成り立つと書きましたが、
減衰が違うことでそのt=0に至るまでの時間差が表れる可能性を考慮していません。)
おまけ3:ロピタルの定理について
臨界減衰が振動せずに0に漸近する説明として
\begin{align*}
X&=te^{\lambda _1 t}\\
&=\frac{t}{e^{-\lambda _1 t}}\\
\lim _{t \to \infty}X&=0~~~(\because logx \lll x^a \lll a^x ~~x \to \infty)
\end{align*}
と書きましたが、これはlogx \lll x^a \lll a^x ~~x \to \inftyが自明だとして
導きました。
これでは納得できないという方もいると思いますので、
ロピタルの定理という便利な定理を紹介し、そちらを使って極限を求めてみます。
ロピタルの定理
ある\frac{f(x)}{g(x)}について、あるc(実数または正の無限大または負の無限大)において
①\lim_{x \to c}=\lim_{x \to c}=0 または \lim_{x \to c}=\pm\lim_{x \to c}=\pm \infty
②cを含む開区間のcを除く点でg'(x)≠0である
の条件を満たすとき
\lim_{x \to c}\frac{f(x)}{g(x)}=\lim_{x \to c}\frac{f'(x)}{g'(x)}=L\\~~\\
ただしLは実数または正の無限大、または負の無限大
中身については私は全然理解していないので、基本Wikipediaにある内容を書き直しただけです。
こちらを使用すると今回の場合
\begin{align*}
f(t)&=t\\
g(t)&=e^{-\lambda_1t}\\~~\\
c&=\infty\\
\lim_{t \to \infty}f(t)&=\lim_{t \to \infty}t=\infty\\
\lim_{t \to \infty}g(t)&=\lim_{t \to \infty}e^{-\lambda _1 t}=\infty ~~(\because\lambda_1 <0)\\
g'(t)&=-\lambda _1 e^{-\lambda _1 t} \neq 0
\end{align*}となり①、②を満たしているので
\begin{align*}
\lim _{t \to \infty}X=&\lim_{t \to \infty}\frac{f(t)}{g(t)}\\
=&\lim_{t \to \infty}\frac{f'(t)}{g'(t)}\\
=&\lim_{t \to \infty}\frac{1}{-\lambda _1e^{-\lambda _1t}}\\
=&0
\end{align*}が成り立ちます。
こちらは極限を調べる際にとても重宝する定理のようなので、
存在だけでも覚えておくとよいかもしれません。