前回の記事では、一般的な回転運動の取り扱い方の説明をし、
そこから導かれる現象として、3次元空間で2軸以上の回転運動を扱う場合、
ジャイロ効果(ジャイロモーメント)と呼ばれる現象が発生するということを説明しました。
今回はそのジャイロ効果が回転体の振動にどのような影響を与えるのかを
見ていきたいと思います。
内容についてある程度理解しているつもりでしたが、詳しく見てみると
分からないところも多かったので、今回から
「回転体力学の基礎と制振 石田・池田 共著 コロナ社」も参考にしています。
今回の記事で回転機械の振動についてはとりあえず一旦終了と思っていましたが、
長くなってしまいましたので、前回同様後半を別記事にしました。
一応内容としては区切りになるので、別の記事として公開しますが、
こちらの記事を前提とした話もありますので、是非順番に見てみてください。
ジャイロ効果とは
ここまでジャイロ効果という言葉の意味を曖昧なまま使用してきたので、
まずはジャイロ効果とは何かを説明したいと思います。
日本語版Wikipediaによると
自転回転する物体が持つ、
- 外部からモーメントが加わっていないかぎり自転軸の方向を保つ性質
- 自転の角運動量が大きいほど姿勢を変えにくい性質
- 外部から自転軸を回すようにモーメントが加えられるとき、
モーメント軸および自転軸の両方と直交する軸について振れ回り運動をする性質
というのが学術上の意味になるそうです。(’21/06/27現在)
その発生メカニズムについてもWikipediaに載っていますが、ここでも説明します。
ジャイロ効果(ジャイロモーメント)の発生原理
まずは自転する物体として独楽を考えてみます。

図では分かりにくいですが、角速度ベクトル\bm{\omega}が上向きですので、
独楽を上から見たときに反時計周りに回転する物体を考えています。
独楽の慣性主軸の1つは回転軸と一致しており、この方向の慣性モーメントをIpとします。
それと垂直になる慣性主軸方向の慣性モーメントをIdとします。
(軸対称な独楽を考えているので、Idは回転軸に垂直な平面上のどのような方向にとっても
一定となります。)
このような独楽が倒れずに長く回転し続けることは皆さんも経験上知っていると思いまが、
実はこれはジャイロ効果の自転軸を保つ性質によるものです。
(厳密には、独楽は多少傾いた状態から回転運動を始めても、
直立状態で安定するように運動しますが、これは今回説明する現象とは少し違います。
ただし原理は一緒のものです。)
では独楽が倒れそうになった時にどのような現象が起きるのか見てみましょう。
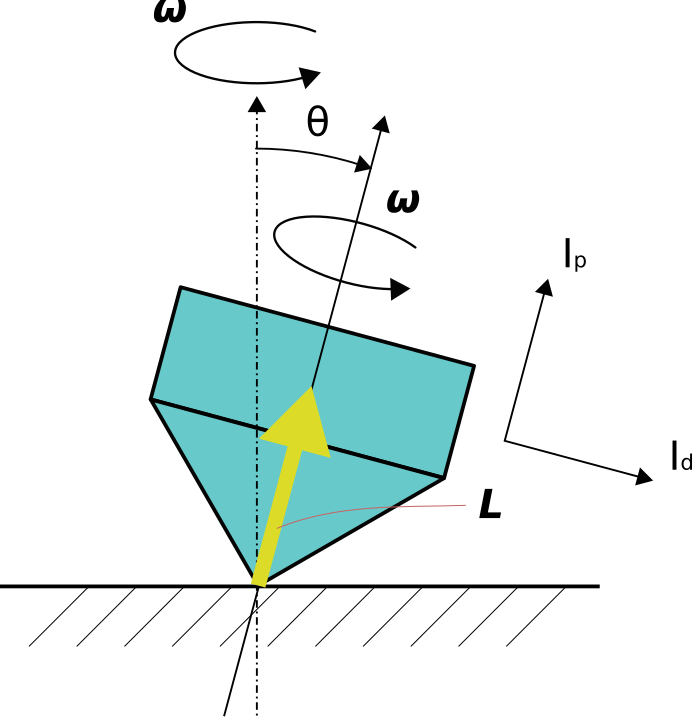
図の様に独楽を角度\theta傾けます。
回転軸と独楽の慣性主軸が一致しているので、独楽の角運動量は回転軸と一致しています。
回転軸と慣性主軸は独楽と一緒に傾きますが、同時に全体としては元の回転軸周りに
振れ回り続けます。
(これについては感覚的には分かりますが、根拠がやや薄いと思います。
とりあえず認めて先に進めましょう。)
角運動量が元の回転軸と傾いたまま回転するということは、
前回までの記事でも描いたように角運動量が振れ回り、時間により変化することになります。
下図は振れ回り運動をする独楽を上から見た図です。
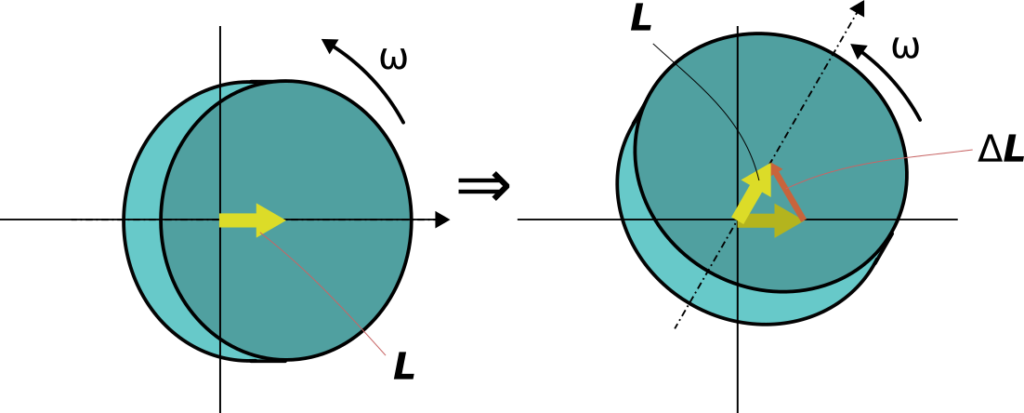
図の様に角運動量が振れ回り角運動量の変化量\Delta\bm{L}が現れます。
回転運動に関する運動方程式は
\frac{d\bm{L}}{dt}=\bm{T}なので、\Delta\bm{L}が存在するということは、それと同じ方向のトルクが
作用しているということになります。
図では回転角を大きく表現していますが、微小時間dtでの回転を考えると、
\Delta\bm{L}は元の角運動量と垂直になります。
(一応後で計算でも示します。)
トルクや角運動量は回転軸で方向を示すので、元の角運動量に垂直ということは
下図のように物体が傾いている平面上のトルクということになります。
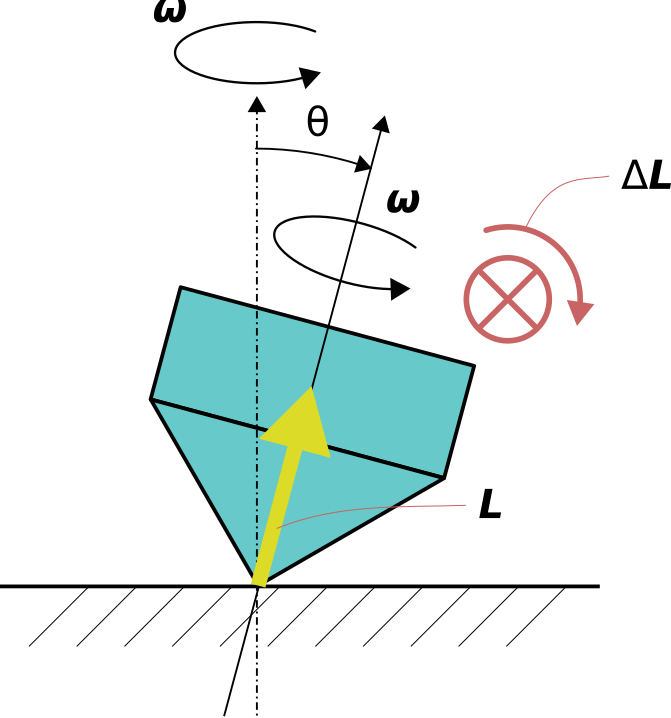
これが意味するところは、回転体が回転軸と角度をなして振れ回るためには、
傾きと同じ方向にトルクが必要ということです。
注意してほしいのは
- 傾けるためにトルクが必要なだけでなく、傾いたまま回転(公転)し続けるためにトルクが必要
- 逆に言うと、傾きと同じ方向にトルクがなければ傾いたまま回転(公転)し続けられないため、
独楽の傾きは小さくなる
(⇒見た目上傾きを小さくするようなトルクが掛かっているように見える
:ジャイロモーメント)
ということです。直感的なイメージと違って、
トルクが作用することで初めて傾きが維持できるので、
回転体を傾け続けるためのトルク
= 物体を傾けるためのトルク + 物体の傾きを維持するためのトルク
となり、物体を傾けるために、回転していないときよりも大きなトルクが必要となります。
これは物体から見ると、見かけ上回転(傾き)ばねが硬くなったとみなされます。
ばねが硬くなるとばね定数を用いて表される共振周波数\omega_n=\sqrt{k/m}が変化します。
これがジャイロ効果が振動に与える影響です。
ジャイロ効果が振動に与える影響はここまで説明した通りですので、
回転体において共振周波数が変化する原理を概念的に理解したいという方には
これまでの説明でとりあえず十分かなと思います。
ただ、一応ジャイロ効果により発生するジャイロモーメントや、
そのモーメントによる共振周波数への影響は理論的・数学的にまとめられているので、
その説明をしていきたいと思います。
ジャイロモーメントの計算
(オイラーの運動方程式を用いた導出)
下図のような独楽について、重心の運動を考えずに重心周りの回転のみを考えます。
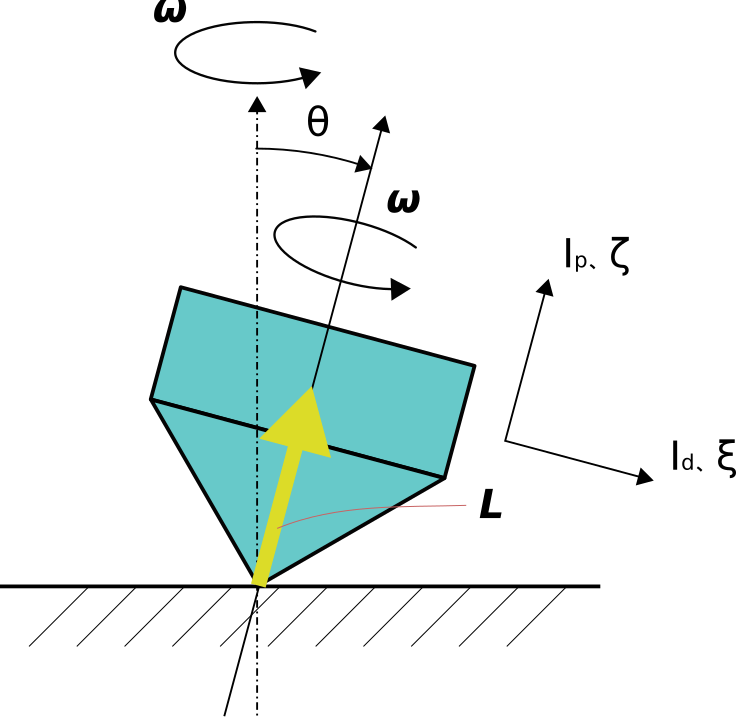
今回の物体は傾くことで、慣性主軸の方向が固定座標系の軸と一致しなくなるので、
前回の記事で紹介したオイラーの運動方程式を用いて慣性主軸方向に作用するトルクを
計算していきます。
(もちろん慣性テンソルの時間変化を考慮すれば固定座標系でも計算することができます。)
オイラーの運動方程式を立てるためには各慣性主軸方向の角速度が分かればよいので、
まずはG-\xi\eta\zetaの定義と、それぞれの軸について角速度を求めます。
\zetaは図中にある通り、物体の自転軸とします。
他の2軸\xi、\eta は、今回扱うような軸対称の物体では、
\zetaに垂直などの方向にでも取ることができます。
自転周期と公転周期がどちらも\omegaで一致しているので、方向を調整することで
軸\xiは常に傾き\thetaと常に同一平面に固定することができます。
(上図にもそのように表記しています。)
ただし、物体が軸対称でなかったり、自転角速度\omegaと公転角速度\Omegaが異なる場合には
\xi軸と傾き\thetaが同一平面上にあるとは限りません。
今回はまずはこのような場合も含めてジャイロモーメントを求めてみましょう。
(まずは軸対称でないと考えて、I_p、I_dではなく、I_\xi、I_\eta、I_\zetaを用います。)
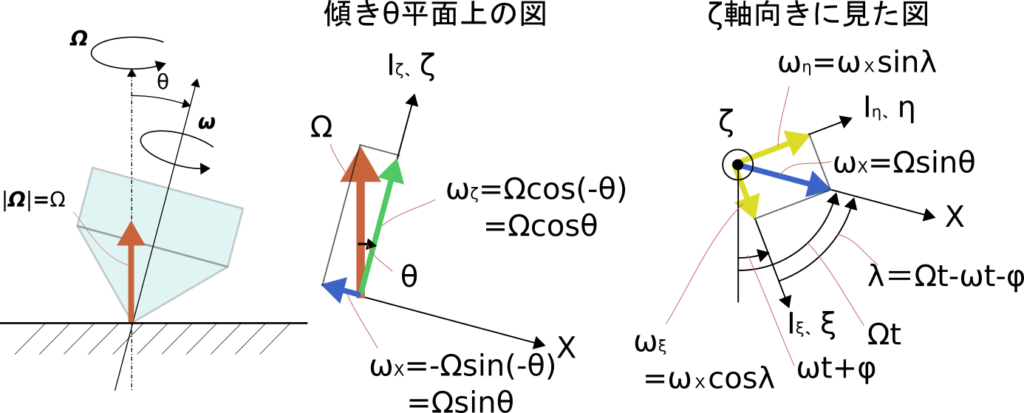
上図の様に公転角速度\bm{\Omega}を各軸成分に分解します。
傾き方向と一致する仮の軸X自身も静止座標系に対して公転角速度\bm{\Omega}で公転しており、
同時に物体も\bm{\omega}で自転しているので、これら2つの軸が
作る角度\lambdaは図の通り\lambda=\Omega t - \omega t - \phiとなります。
ただし\phiはt=0のときにX軸と\xi軸なす角(位相差)を表しています。
また、図の途中で\omega _Xの向きが逆になっていますが、
符号等を正しく考慮するためにあえて正方向にベクトルを表示しています。
\zeta軸回り自転成分\omegaの扱いについては正直とても悩みました。
色々調べた結果、回転座標上に静止すると公転と逆向きに回転しているようにとられられるので、
\omega-\Omegaとして考えるのが良いようです。
(ここで\Omegaを考慮するなら\Omega cos\thetaは必要なのか?等
色々考えましたが、最終的には記事の最初に挙げた文献の内容を正としています。)
この結果をまとめると、座標系G-\xi\eta\zetaにおける角運動量の各成分は
\begin{align*}
\bm{ω}^{*}=\begin{pmatrix}\omega_\xi \\ \omega _\eta \\ \omega _\zeta)\end{pmatrix}=
\begin{pmatrix}
\Omega sin \theta cos((\Omega - \omega)t-\phi) \\
\Omega sin \theta sin((\Omega - \omega)t-\phi)\\
\Omega cos \theta+(\omega -\Omega)
\end{pmatrix}
\end{align*}となります。またこれらの時間微分は
\begin{align*}
\bm{ω}'^{*}=\begin{pmatrix}\omega' _\xi \\ \omega' _\eta \\ \omega' _\zeta\end{pmatrix}=
\begin{pmatrix}
-\Omega(\Omega - \omega) sin \theta sin((\Omega - \omega)t-\phi) \\
\Omega (\Omega-\omega) sin \theta cos((\Omega - \omega)t-\phi)\\
0
\end{pmatrix}
\end{align*}となります。これらをオイラーの運動方程式に代入していきます。
オイラーの運動方程式は
\begin{align*}
I_\xi \omega'_\xi-(I_\eta-I_\zeta)\omega_\eta \omega_\zeta=&T_\xi\\
I_\eta \omega'_\eta-(I_\zeta-I_\xi)\omega_\zeta \omega_\xi=&T_\eta\\
I_\zeta \omega'_\zeta-(I_\xi-I_\eta)\omega_\xi \omega_\eta=&T_\zeta\\
\end{align*}
なので
\begin{align*}
-I_\xi\Omega(\Omega - \omega) sin \theta sin((\Omega - \omega)t-\phi)-
(I_\eta-I_\zeta)(\Omega cos \theta +(\omega - \Omega))\Omega sin\theta sin((\Omega - \omega)t-\phi)=&T_\xi\\
I_\eta\Omega (\Omega-\omega) sin \theta cos((\Omega - \omega)t-\phi)-
(I_\zeta-I_\xi)(\Omega cos \theta +(\omega - \Omega))\Omega sin\theta cos((\Omega - \omega)t-\phi)=&T_\eta\\
-(I_\xi -I_\eta)\Omega ^2sin^2\theta sin((\Omega - \omega)t-\phi)cos((\Omega - \omega)t-\phi)=&T_\zeta\\
\end{align*}
となります。
\zeta軸についてはI_\xi = I_\etaなので0となりますが、
一応表記してあります。軸対称でないものについてはこちらの計算も必要になります。
さらにこちらをまとめると
\begin{align*}
-\Omega sin \theta sin((\Omega - \omega)t-\phi)\{I_\xi (\Omega - \omega) +(I_\eta-I_\zeta)(\Omega cos \theta+(\omega -\Omega )) \}=&T_\xi\\
\Omega sin \theta cos((\Omega - \omega)t-\phi)\{I_\eta (\Omega-\omega) +(I_\xi-I_\zeta)(\Omega cos \theta +(\omega - \Omega))\}=&T_\eta\\
-(I_\xi -I_\eta)\Omega ^2sin^2\theta sin((\Omega - \omega)t-\phi)cos((\Omega - \omega)t -\phi)=&T_\zeta\\
\end{align*}
となり、これがジャイロモーメントを表す式になります。
ただし、今回考えるのは\omega=\Omegaでなので、こちらを代入すると
\begin{align*}
\Omega^2 (I_\eta-I_\zeta)sin \theta cos \theta sin\phi=&T_\xi\\
\Omega^2 (I_\xi-I_\zeta)sin \theta cos \theta cos\phi =&T_\eta\\
(I_\xi -I_\eta)\Omega ^2sin^2\theta sin\phi cos\phi=&T_\zeta\\
\end{align*}
となります。更に今回扱うような軸対称な独楽では、各軸の慣性モーメントは
I_\xi=I_d,~~I_\eta=I_d,~~I_\zeta=I_p
であり、\xi、\etaの方向は\zetaに垂直な任意の方向に選ぶことができるため、
\phi=0とすることができます。これにより
\begin{align*}
0=&T_\xi\\
\Omega^2 (I_d-I_p)sin \theta cos \theta =&T_\eta\\
0=&T_\zeta\\
\end{align*}
となります。こちらが一般的なジャイロモーメントと呼ばれるトルクになります。
ジャイロモーメントについて更に考えてみる
得られた結果を更に詳しく見てみます。
軸対称のとき、ジャイロモーメント(トルク)の大きさは
|\bm{T}|=|\Omega^2 (I_d-I_p)sin \theta cos \theta|ですが、軸対称ではないがI_\xi=I_\etaのときはどうでしょうか。
軸対称でない場合(I_\xi=I_\eta、\phi \neq 0)
このときの各軸回りのトルク(ジャイロモーメント)は
\begin{align*}
\Omega^2 (I_d-I_p)sin \theta cos \theta sin\phi=&T_\xi\\
\Omega^2 (I_d-I_p)sin \theta cos \theta cos\phi =&T_\eta\\
0=&T_\zeta\\
\end{align*}
であり、トルクの大きさ|\bm{T}|=\sqrt{T^2_\xi+T^2_\eta+T^2 _\zeta}なので
\begin{align*}
|\bm{T}|=&\sqrt{(\Omega^2 (I_d-I_p)sin \theta cos \theta)^2(sin^2\phi + cos^2\phi)}\\
=&|\Omega^2 (I_d-I_p)sin \theta cos \theta|\\
\end{align*}となり、軸対称の時と同じになります。
また、方向についても元々\phiは傾き\thetaの平面との位相差(ずれ)なので、
傾き\thetaの平面に対して垂直方向であり、軸対称の場合と同じになります。
方向性があるが、傾き\thetaと慣性主軸方向が一致している場合
(I_\xi \neq I_\eta、\phi =0)
次はI_\xi \neq I_\etaのような方向による形状の差が大きい物体を傾ける場合を考えます。
ただし傾ける方向は慣性主軸\xiに向かって傾けます。
(回転ベクトルで表すと\etaの方向です。)
これは\phi=0ということなので、各軸回りのトルク(ジャイロモーメント)は
\begin{align*}
0=&T_\xi\\
\Omega^2 (I_\xi-I_\zeta)sin \theta cos \theta =&T_\eta\\
0=&T_\zeta\\
\end{align*}
となります。
こちらもI_\xi=I_d、I_\zeta=I_pとおけば
|\bm{T}|=|\Omega^2 (I_d-I_p)sin \theta cos \theta|であり、方向は傾き\thetaの平面に対して垂直方向となります。
意味するところは軸対称の場合とほぼ同じになります。
方向性があり、傾き\thetaと慣性主軸方向が一致しない場合
(I_\xi \neq I_\eta、\phi \neq 0)
方向による形状の差が大きい物体が、慣性主軸ではない方向に傾けられて
回転する場合はどうでしょうか。
このときの各軸回りのトルク(ジャイロモーメント)は上で求めたそのままで
\begin{align*}
\Omega^2 (I_\eta-I_\zeta)sin \theta cos \theta sin\phi=&T_\xi\\
\Omega^2 (I_\xi-I_\zeta)sin \theta cos \theta cos\phi =&T_\eta\\
(I_\xi -I_\eta)\Omega ^2sin^2\theta sin\phi cos\phi=&T_\zeta\\
\end{align*}
となります。
軸対称で、公転速度と自転速度が一致しない場合
(I_\xi = I_\eta=I_d、\Omega \neq \omega)
円柱のような軸対称の物体が自転速度と公転速度が異なる状態で回転運動している場合は
\begin{align*}
-\Omega sin \theta sin((\Omega - \omega)t-\phi)\{ I_d\Omega cos \theta -I_p(\Omega cos \theta+(\omega -\Omega )) \}=&T_\xi\\
\Omega sin \theta cos((\Omega - \omega)t-\phi)\{I_d\Omega cos \theta -I_p(\Omega cos \theta +(\omega - \Omega))\}=&T_\eta\\
0=&T_\zeta\\
\end{align*}
となります。
\Omega \neq \omega の場合では傾き平面と\xi\eta軸が一致しないため分かりずらいですが、
ここで(\Omega -\omega )t -\phi)は傾き平面と\zeta-\xi平面の成す角を表しています。
sin、cosの関係を考慮すると、結局この時のトルク(ジャイロモーメント)は傾き平面に対して
常に垂直になり、その大きさは
|\bm{T}|=|\Omega sin \theta \{ I_d\Omega cos \theta -I_p(\Omega cos \theta+(\omega -\Omega )) \}|となります。
もう一つのジャイロモーメント
今回ジャイロモーメントについて説明するにあたり、いくつかの資料を調べてみましたが、
そもそもジャイロモーメントやジャイロ効果についての定義は割と曖昧なようです。
その中で、ジャイロモーメントとして
T =-I_p\omega \Omega sin \theta\approx -I_p\omega \Omega \theta
というような表記をよく見かけました。
これは上で説明したジャイロモーメントとは異なります。
これについてはかなり悩みましたが、結局下記のようなことのようです。
まず自転がない場合を考えます(\omega =0)。このときの各軸周りのモーメントは
\begin{align*}
-\Omega sin \theta sin(\Omega t-\phi)\{I_\xi \Omega +(I_\eta-I_\zeta)(\Omega cos \theta -\Omega ) \}=&T_\xi|_{\omega = 0}\\
\Omega sin \theta cos(\Omega t-\phi)\{I_\eta \Omega +(I_\xi-I_\zeta)(\Omega cos \theta -\Omega)\}=&T_\eta|_{\omega = 0}\\
-(I_\xi -I_\eta)\Omega ^2sin^2\theta sin(\Omega t-\phi)cos(\Omega t -\phi)=&T_\zeta|_{\omega = 0}\\
\end{align*}
となります。
また、これらの多くの文献では軸対称の物体を扱っているので(I_\xi= I_\eta =I_d)、
上の「軸対称で、公転速度と自転速度が一致しない場合」で説明した通り
T_\xi、T_\etaは常に傾き平面に垂直になります。
この方向をY(傾き平面方向で\zetaと垂直な方向をX)とすると
\begin{align*}
T_X|_{\omega =0}=&0\\
T_Y|_{\omega =0}=&\Omega sin \theta \{I_d \Omega cos\theta -I_p(\Omega cos \theta -\Omega ) \}\\
T_\zeta|_{\omega = 0}=&0
\end{align*}これらのモーメントと、元の\omega \neq 0のときのモーメントの差を取ります。
元のモーメントも同様に
\begin{align*}
T_X=&0\\
T_Y=&\Omega sin \theta \{ I_d\Omega cos \theta -I_p(\Omega cos \theta+(\omega -\Omega )) \}\\
T_\zeta=&0
\end{align*}となります。これらの差を取ると
\begin{align*}
T_X-T_X|_{\omega = 0}=&0\\
T_Y-T_Y|_{\omega = 0}=&-I_p\omega \Omega sin \theta\\
T_\zeta-T_\zeta|_{\omega = 0}=&0\\
\end{align*}となります。
こちらの差分を持ってジャイロモーメントと呼ぶ場合もある、ということのようです。
なぜこのような2種類の定義の仕方があるかというと、
物体を慣性主軸から傾けて回転運動をさせた時点で
回転軸方向以外のモーメントが発生するためです。
(このような現象は、全く同じ現象ではないですが、以前の記事でも紹介しました。)
自転している物体が公転することで発生する現象がジャイロ効果であるとするならば、
自転の影響により発生するモーメントのみをジャイロモーメントとするのが
今回2つ目に説明した定義になります。
まとめ
今回はジャイロ効果と呼ばれる現象と、それが振動にどのような影響を与えるのかについて
簡単に説明しました。
一言で言ってしまえば、回転体はジャイロ効果で見た目上傾き方向に硬くなり、
傾きを含む共振モードの共振周波数が高くなるという現象が現れます。
また、結果として現れるジャイロモーメントと呼ばれるモーメントについても
実際に導出しました。
ジャイロモーメントについては具体的に詳しく触れている教科書等はあまり見当たらず、
確認を取るのに苦労しましたが、
上にも挙げた 「回転体力学の基礎と制振 石田・池田 共著 コロナ社」は
この辺りの具体的な内容に触れている良い文献だと思います。
私の拙い知識では間違っている部分もあるかもしれませんので、
疑問を持った方やより詳しく知りたい方はこちらを読んでみるとよいかもしれません。
また、この本は「回転機械の力学 山本・石田 共著 コロナ社」の内容を
より平易に書いたもののようですので、こちらも参考になるかもしれません。
(私は不勉強で読んでいませんが・・・)
次回は今回導出したジャイロモーメントを導入した、
傾きの運動方程式を導出していきたいと思います。