前回の記事では回転体の振動における特徴的な現象の一つである自動調心作用について
説明しました。
今回からは回転体の振動でしばしば現れ、特徴的な現象を引き起こす、
傾きを考慮する場合の振動について説明していきたいと思います。
回転運動の基礎まで説明したかったのですが、説明が思った以上に
長くなってしまいましたので前後編としたいと思います。
前編では傾き振動を扱う具体的な方法についてあまり詳しく書いておらず、
提示した問題に対する解決策を十分に提示できていないと思います。
また、後編では前編を前提とした説明をしていますので、
是非前後編を合わせて読んでいただけると良いと思います。
(後編はこちら)
1次元の傾き振動
物体が傾くためには最低でも2次元空間を考える必要があるので、
1次元の傾き振動というと少し変な感じがしますが、
これは傾く方向が1次元のみという意味です。
具体的には下図のようなものになります。
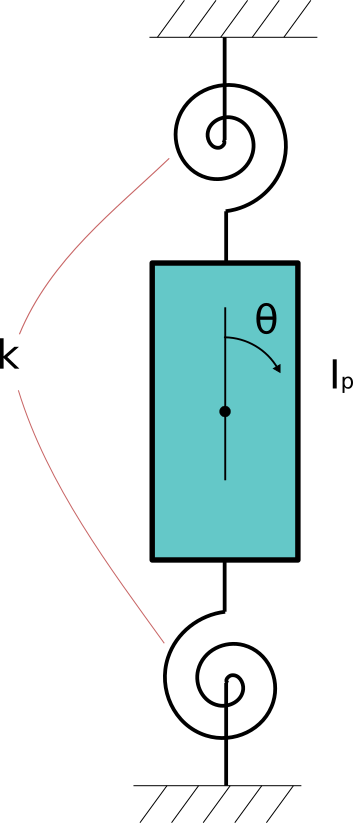
慣性モーメントI_pの物体が上下の壁に回転ばねで接続されており、
回転ばねは上下合わせてばね定数kで、傾き\thetaに対してT=k\thetaとなる
トルクTを作用させます。
回転運動の基本を学んだことがある方は知っていると思いますが、
慣性モーメントとは回転運動における質量の様なものです。
(後で詳しく説明します。)
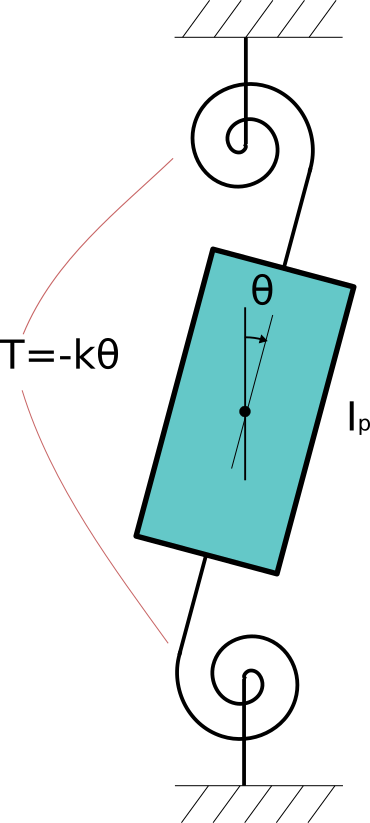
このようなモデルの回転運動の方程式は
\begin{align*}
I_p\theta''=&T\\
=&-k\theta
\end{align*}となります。\theta''の部分は\omega'と書かれている場合もあります。
また、左辺を(I_p \omega)'として学んでいる方もいるかもしれません。
その場合も、今回の様な1次元の回転運動を扱う場合にはI_pが一定なので結果は同じになります。
この運動方程式をこれまで扱ってきた並進運動の運動方程式と見比べると
\begin{align*}
並進運動:~&mx''=F=-kx\\
回転運動:~&I_p\theta''=T=-k\theta\\
\end{align*}となり、質量mと慣性モーメントI_p、変位xと角度\theta、
外力Fと外力のモーメントTが対応したほぼ同じ式になることが分かります。
また、角速度に比例した粘性減衰cを考えた場合にも
\begin{align*}
並進運動:~&mx''=F=-kx-cx'\\
回転運動:~&I_p\theta''=T=-k\theta-c\theta'\\
\end{align*}となり、ここから得られる運動は並進運動の場合と同じく、振動運動になることが分かります。
(減衰比が大きい場合は振動せずに過減衰運動となります。)
減衰がない場合のθの一般解は
\theta=Acos(\omega_n t-\phi)\\
A,\phiは定数、\omega_n=\sqrt{\frac{k}{I_p}}となり並進運動と同じ様に表せます。
2次元の傾き振動
これまでの説明から、回転運動も並進運動と同じ様に捉えている方が
多いのではないかと思います。
実際にそれは正しいのですが、それが成り立つのは1次元の傾き振動を考える場合のみです。
ここからは2次元の傾き振動について考えてみましょう。
並進運動では、2次元空間での運動を以下の様に考えました。
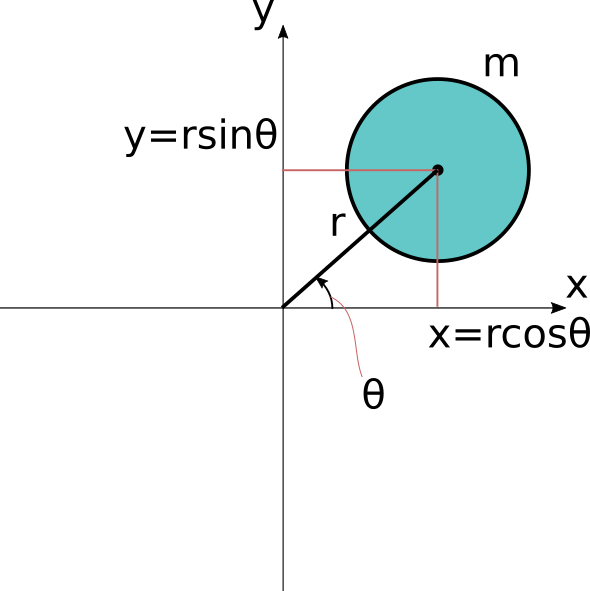
上図の様に並進運動はxとyでそれぞれに分離して考えられるので
mx''=-kx\\ my''=-ky
としてそれぞれを解きました。
では、傾きについて同じ様に考えてみます。
例として先ほどと同じ様な下図のモデルを考えます。
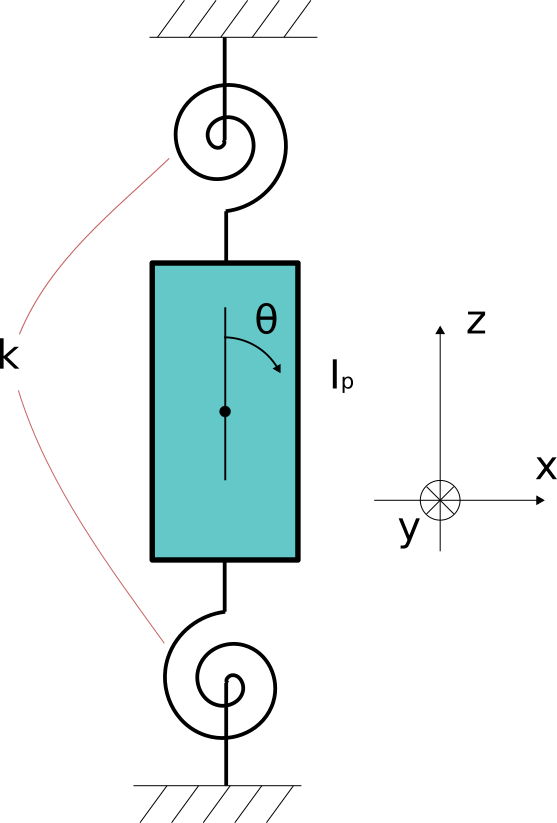
今回の物体は傾き\thetaをx-y平面上にとることができます。
また、説明を簡単にするため、物体はz軸に関して対称な円筒です。
ここで一応説明しておくと、2次元以上の回転運動では回転の方向を表現するのが難しいため、
回転やトルクの方向は回転軸方向で表現します。
例えばこれまで扱ってきたような画面と平行に回転する運動の場合、
今回の例ではy軸方向の回転運動ということになります。
また、回転の方向は右ねじの方向が正となります。
これは通常の3次元座標系が右ねじに沿って設定されているためです。
(x軸→y軸という風に回転させたときの右ねじ軸方向がz軸になるように
x,y,z軸が設定されています。
x→y→z→x→…なので、y軸周りの回転ではz軸→x軸と回転させる方向が正となります。)
このようなモデルで並進運動と同じ様にx、y方向に分離して運動を考えられるかというと、
厳密にはできません。
簡単な例として、x軸周りの傾きが90°、y軸周りの傾きが90°である場合を考えてみましょう。
そもそもこれはどのような状態を表しているのでしょうか。
少し考えてみます。
①x軸周りに回転させた後、y軸周りに回転させる
これはすぐに良くない例だと分かります。
実際に回転させてみると下図のようになります。
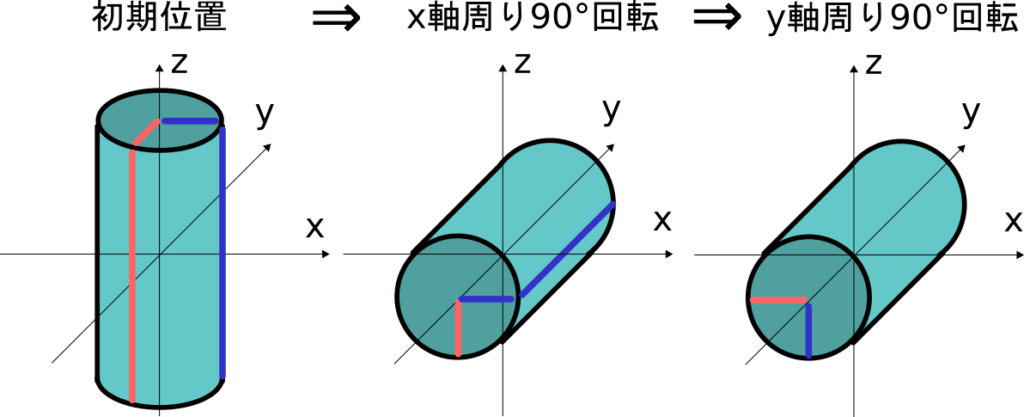
これをy軸とx軸の回転を逆にすると下図のようになります。
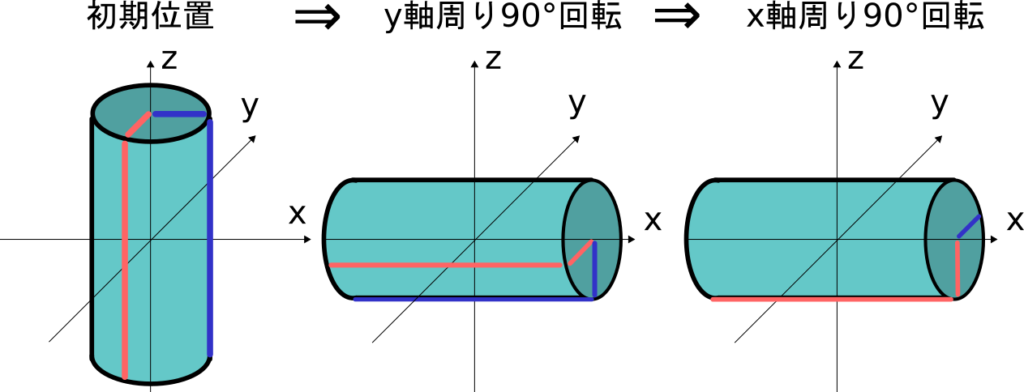
結果が変わってしまっていることがすぐに分かると思います。
x軸周りに\theta _x回転、y軸周りに\theta _y回転という方法では
物体の姿勢を表現するのに適切ではありません。
②各平面に投影した角度で表現する
y-z平面へ投影したときの角度を\theta _x(x軸周り)、
z-x平面へ投影したときの角度を\theta _y(y軸周り)とすれば、
一応物体の姿勢は決まると思います。
\theta _x=\theta_y = 90°のときは下図の様な姿勢になります。
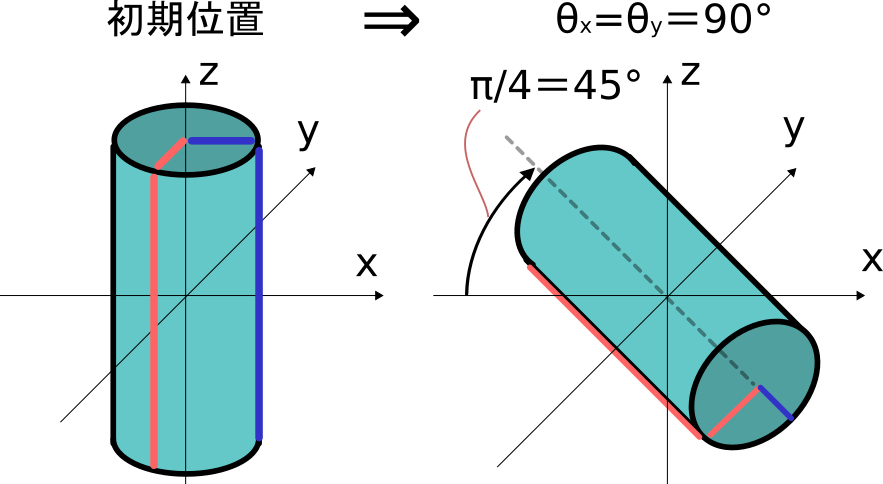
実際には円筒の軸がx-y平面上にあればどの姿勢でも\theta _x=\theta_y = 90°を
満たしますが、\theta _x=\theta_y = 89.999…°からの連続性を考えると
図の様な位置にするのが良いと思います。
姿勢は決まりますが、45°などはどこから出てきたのかもよく分かりません。
(実際は\theta _x、\theta_y の関係から総合的に決まる角度です。)
表現は可能ですが、物理的に扱いやすい意味を持った数字かと言われると疑問です。
③角度をベクトル的に足す
回転の角度や角速度はベクトルなので、各軸の回転はベクトル的に足すことができます。
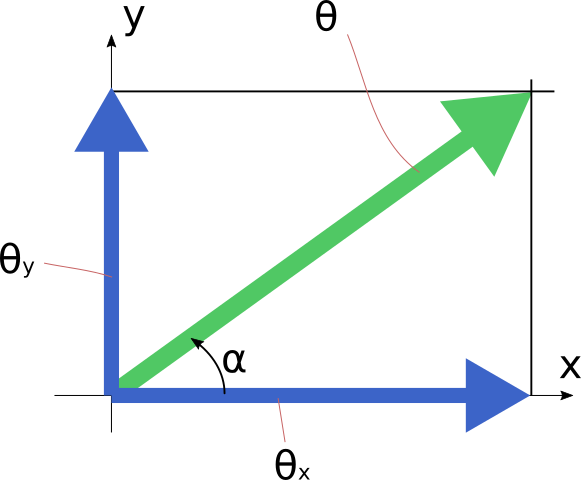
\theta _x=\theta_y = 90°=\pi/2のときベクトルθはα=45°で、
大きさが\sqrt{\theta ^2 _x=\theta ^2 _y} = \frac{\sqrt{2}}{2}\pi \fallingdotseq 127°となります。
これはを図に表すと下図の様になります。
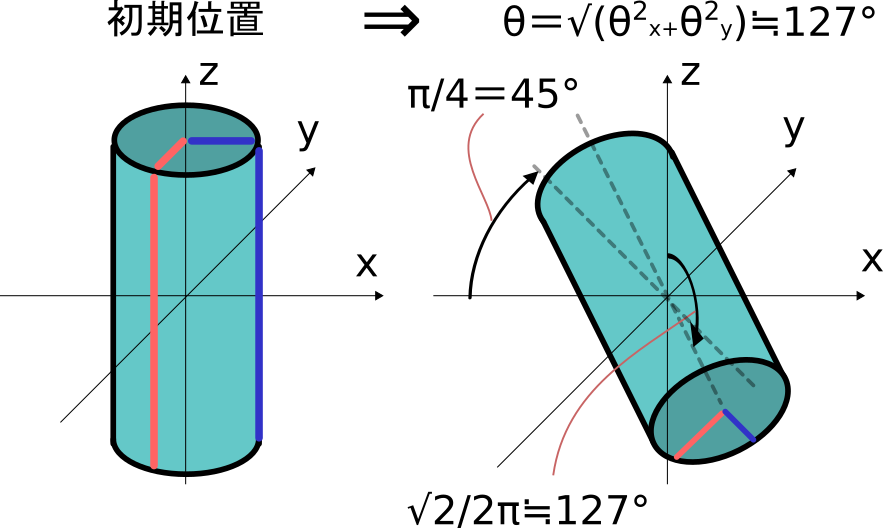
これは角度がベクトルであることを考えればとても全うな考え方だと思います。
ただし、x,y各軸について90°傾けた結果がx-y平面を突っ切って
逆側まで回転するというのは感覚とは全く異なっており、
あまり物理的に良い表現ではないように思います。
結局どのように表現するのが良いのか(工学的方法)
「結局どうすれば良いのか」という問いの答えをここですぐに出すことはできませんが、
x軸、y軸の様に分けて考えるという方法が向いていないということは分かりました。
正しく回転運動を表現するためには力学に基づいて回転を考えていく必要があります。
(後々説明する予定です。)
ただ、ここでは工学的に用いられる表現方法について説明しておきます。
この方法は傾き\thetaが微小な時に有効です。
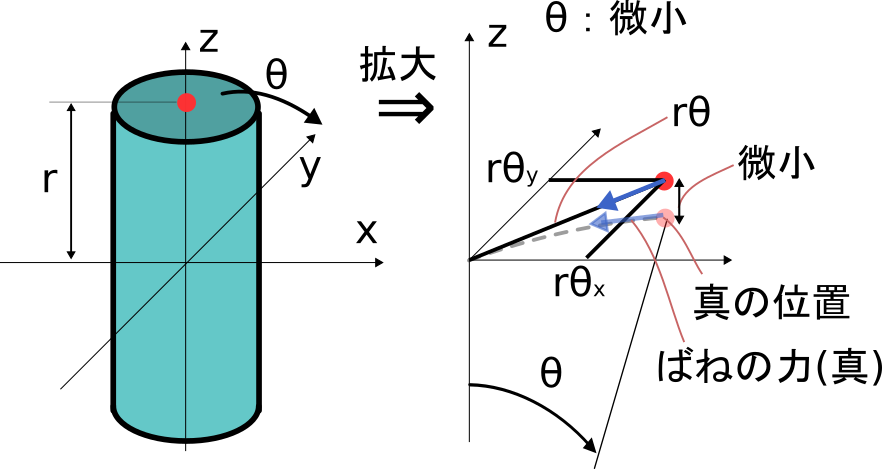
上図の様に\thetaが微小であるとき、回転の描く円弧は直線に限りなく近くなり、
傾きによる変位r\thetaはある平面上での運動になります。
同様にばねによる力も、本来は円弧の接線方向に働きますが、
円弧が平面上の直線に限りなく近くなるためこちらも平面上のr\thetaと
同じ向き(符号はマイナスです)に働くことになります。
このとき、ばねによるトルク T=力(F) × 距離(r)なので、
ばねによる力FはF=T/r=-k \theta /rとなることに注意してください。
平面上での運動ですので、これは並進運動と同様にx、y方向に分離することができます。
これは\thetaが微小であればすべての点について成り立つので、最終的に
\begin{align*}
I_{px}\theta _x=-k\theta_x\\
I_{py}\theta _y=-k\theta_y\\
\end{align*}をそれぞれ解くことで物体の回転運動を求めることができます。
さて、ではこの\thetaが微小という条件はどれくらい
使用可能な条件でしょうか。
工学的に回転体の振動を考える場合、金属材料に関する振動である場合が多いです。
(回転体のシャフトなど)
ご存じの通り金属材料は強度が高く、簡単には大きい傾きは現れません。
(大きな傾き・曲げが発生するときには、破壊に至ってしまう場合が多いです。)
なので、この\thetaが微小という条件は、工学的には十分有用だと考えられます。
ただし、ユニバーサルジョイントなどの大きな傾きが前提となる機械を扱う場合には
この表現方法では不十分である可能性があることに注意してください。
また、この近似は下図の様なものになります。(角度は大げさに描いてあります。)
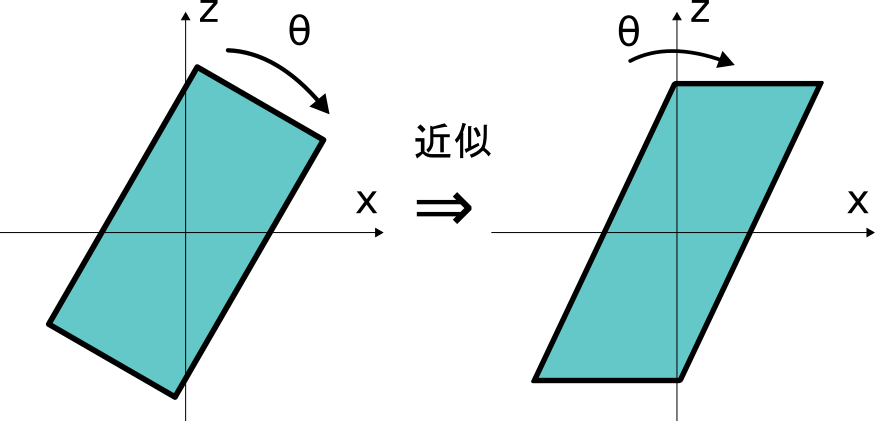
このことから、回転中心から半径方向(上図だとxやy方向)に長い独楽のような形状の
物体等では誤差が大きくなることが予測されます。
この辺りはどの程度ならば実用レベルといった基準はないですが、
自分たちが使用している計算には近似が入っているということを
知った上で結果を利用しましょう。
例えばゴムダンパの傾きなどは金属に比べれば大分大きいと思います。
これを厳密に計算するべきか、誤差を含んだ概算で十分かの判断は状況によります。
必要であれば計算するべきだと思いますが、系が複雑な場合は掛ける労力に見合うかを考慮し、
概算で済ませてしまっても良いと思います。
(そもそもゴムダンパの大変形は一定のばね定数kや粘性減衰係数cでどこまで正確に
表現できているかも疑問です。)
慣性モーメント
ここまで物体の回転位置をx軸,y軸といった視点で考えるのが難しいことを説明しましたが、
もう一つ考えなければならない問題があります。
質量mに相当する慣性モーメントI_pについてです。
ここまで慣性モーメントについて詳しく説明していませんでしたので、
まずは慣性モーメントとは何かから説明します。
慣性モーメントとは
慣性モーメントがなぜ導出されたかは後で説明するとして、
慣性モーメントは以下の式で表されます。
\begin{equation}
I_p=\Sigma r^2m=\int r^2dm
\end{equation}いくつかの質点に分けられる場合は総和を、連続体である場合は積分を使って
上記の様に表されます。rは回転軸からの距離(回転軸におろした垂線の長さ)です。
例として円盤の慣性モーメントを計算してみましょう。
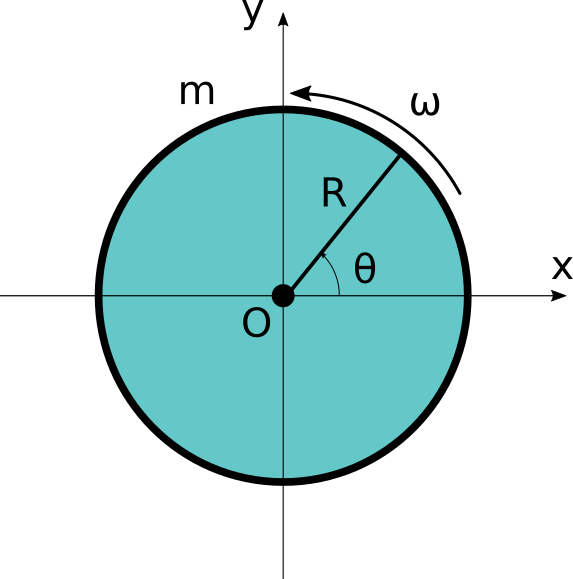
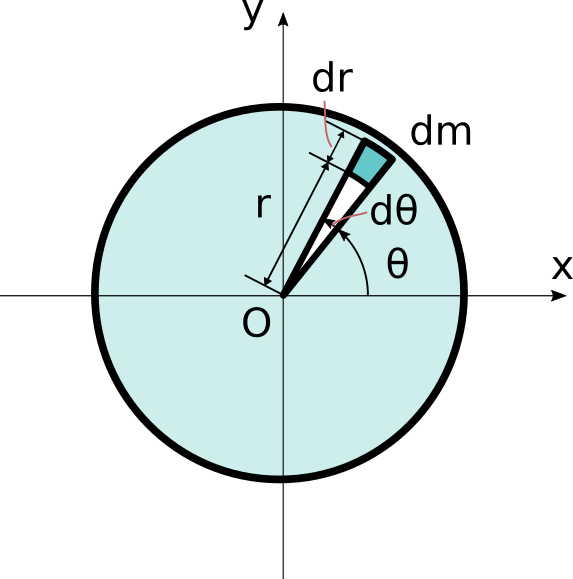
上の左図の様な円盤の慣性モーメントを考えます。
回転方向は画面に垂直な軸周りで、質量は一様で合計がm、半径Rの円盤です。
(厚みは設定していません。)
このような円盤について右図のようにごく小さい一部分を取り出します。
半径r、角度\thetaの位置から半径方向にdr、角度方向にd\thetaだけ取り出し、
その質量はdmです。
まずは質量dmについて計算してみましょう。
円盤の質量は全体でmなので、面積あたりの質量は
\frac{m}{A}=\frac{m}{\pi R^2}となります。
切り出した微小な部分は四角形とみなせるので、その面積は
dA=dr \times rd\theta
なので、最終的にdmは
dm=\frac{m}{A}\times dA=\frac{mr}{\pi R^2}drd\thetaとなります。これらの結果から、慣性モーメントは
I_p=\int r^2dm=\int r^2 \frac{mr}{\pi R^2}drd\thetaとなります。
(r^2は(r+dr/2)^2ではないかと思う方がいるかもしれませんが、
drは微小なのでr^2としてしまって問題ありません。
これは面積を四角形として計算したときもそうですが、
最終的にdr^2、d\theta ^2などの微小項は無視できるとして消してしまいます。)
実際に計算する場合は円盤全体を考えるのでrが0 \to R、\thetaが0 \to 2\piの範囲で積分して
\begin{align*}
I_p=&\int^{2\pi}_0 \!\!\!\! \int_0^R r^2 \frac{mr}{\pi R^2}drd\theta\\
=&\int^{2\pi}_0 \Biggl[\frac{1}{4}\frac{mr^4}{\pi R^2}\Biggr]^R _0 d\theta\\
=&\int^{2\pi}_0 \frac{1}{4}\frac{mR^2}{\pi } d\theta\\
=&\Biggr[ \frac{1}{4}\frac{mR^2}{\pi } \theta \Biggl]^{2\pi}_0\\
=&\frac{mR^2}{2}
\end{align*}となります。これが円盤を軸方向に回転させるときの慣性モーメントです。
2次元傾き振動における慣性モーメント
上で説明したように求められる慣性モーメントですが、
2次元以上の回転運動を考える場合には急に扱いが難しくなります。
例として先ほどと同じ様なモデルを考えます。

さて、このモデルについてx軸方向、y軸方向の慣性モーメントをそれぞれ考えてみましょう。
分かりやすい例としてx軸方向にだけ、\theta_x回転させたものが下図になります。
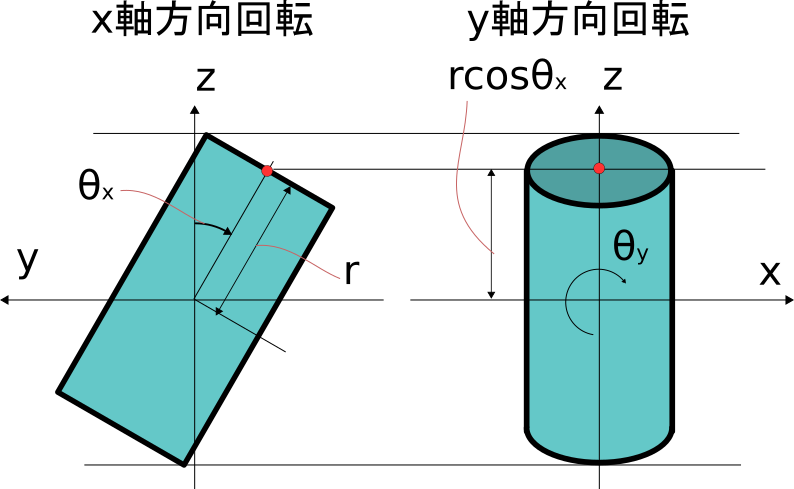
ここで赤い点について見てみましょう。
赤い点は円筒の一番遠い部分を切り出したときのの重心になります。
慣性モーメントI_pはI_p=\Sigma r^2m なので、
切り出した一部についてのx軸周りの慣性モーメントI_{px~out}は
I_{p~out}=r^2m_{out}となります。m_{out}は切り出した一番外側の重量です。
これに対して同じく切り出した一部についてのy軸周りの慣性モーメントI_{py~out}は
図の様に軸からの距離が変化しているため
I_{py~out}=r^2cos^2\theta_x mとなります。
見てわかる通り、y軸周りの回転運動を考えるのに、x軸周りの回転運動が影響してきます。
これは回転位置をx、yで表現できるかどうかという説明のときにもありました。
実はこちらの慣性モーメントの変化も工学的には\bm{\theta}が小さいときには無視されます。
無視していることを知った上で計算結果を利用してください。
結言(中締め?)
ここまで、回転運動を扱うことの難しさについて説明しました。
そしてその難しさへの一応の回答として傾き\bm{\theta}が小さい場合は
並進運動と同様に各軸方向に分解して考えても良いということを示しました。
実際多くの計算ではこの方法が使われており、とても一般的な方法です。
しかし、一般的に使われすぎていてこれが近似を用いた手法であることを意識していない方も
たくさんいるのではないかと思います。
近似を用いた手法はその前提から逸脱すると正しい結果が得られません。
そのような間違いをしないために、裏にどのような理論があるかを理解することは大切だと思います。
また、回転体の振動を考える場合、これまで考えてこなかった最後の1軸に
無視できない大きな回転が加わります。
回転体の振動を扱う以上、これを無視するわけにはいきませんので、
力学分野から回転運動を扱う方法を学びましょう。
後編では力学分野で回転運動を扱う方法について説明します。
後編はこちら