こちらの記事は前後編として構成しており、前編での説明を前提とした説明がいくつかあります。
是非前編と合わせて見てみてください。
(前編はこちら)
回転運動の基本
前編では回転運動が並進運動とは異なるものであることを説明してきました。
そもそも回転運動には2次元以上の空間が必要なので、
2軸以上の回転を別々に考える場合には4次元以上が必要になります。
しかし現実は3次元なので、それぞれが影響する次元が重複して、
お互いに影響を与えることになります。
これまでの説明では工学的にはこれらの影響を無視すると言いました。
しかし、回転体の振動を考える場合、これまで考えてこなかった最後の1軸に
無視できない大きな回転が加わります。
回転体の振動を扱う以上、これを無視するわけにはいきませんので、
力学分野から回転運動を扱う方法を学びましょう。
回転運動の運動方程式導出
まずは回転運動の運動方程式がどのように導出されるかを説明します。
基となるのはこれまでも使ってきた並進運動の運動方程式です。
mx''=F
x、Fはそれぞれ1次元での位置と外力なので、これを3次元のベクトル\bm{r,F}で表現します。
m\bm{r}''=\bm{F}今回は原点に関する回転を考えるので、原点周りの回転方向成分
(原点を中心とした円の接線方向の成分)のみを取り出します。
具体的には両辺について、\bm{r}との外積を取ります。
(左側から\bm{r}を外積演算します。)
外積について一応説明すると以下のような演算です。
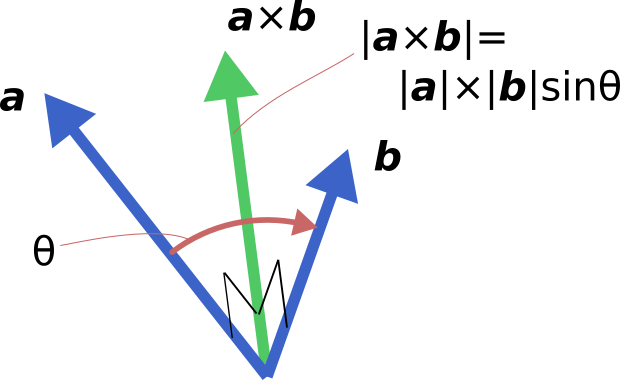
上図の様に、外積は二つのベクトル両方に
垂直なベクトルが得られる演算で、多くの場合" \times "で表されます。
外積演算後のベクトルの大きさは|\bm{a}|\times|\bm{b}|sin\thetaとなります。
(\thetaは2つのベクトルのなす角)
|\bm{b}|sin\thetaはベクトル\bm{b}の、ベクトル\bm{a}に垂直な成分なので、外積は2つのベクトルに垂直方向で、
大きさが2つの垂直成分の積となるベクトルが得られるということになります。.
また、図の通り演算に順番があるため一般に\bm{a} \times \bm{b} =- \bm{b} \times \bm{a}となり、
積の交換法則は成り立ちません。
\bm{r}は物体の位置を表すとともに、\bm{r}-\bm{0}なので、
原点から物体への方向を表すベクトルでもあります。
これらのことから、\bm{r}との外積を取るということは下図のように
原点周りの成分(原点を中心とした円の接線方向の成分)を取り出したことになります。
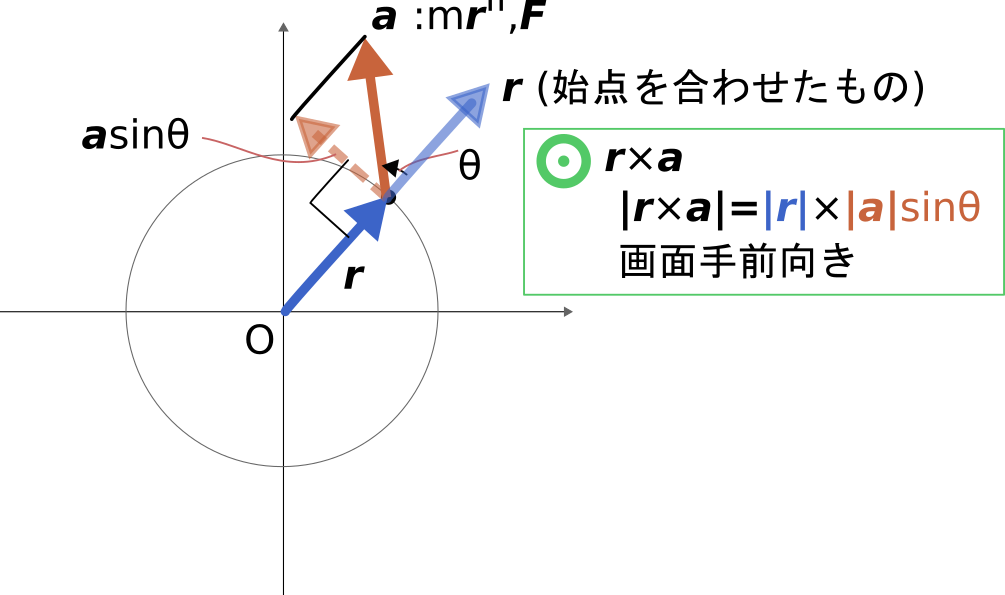
図中のaはm\bm{r}''であったり、外力\bm{F}であったりですが、
どちらでも\bm{r}に垂直な成分のみが取り出されます。
また、外積\bm{r} \times \bm{a}の向きは画面手前向きとなります。
図中の記号は紙面に垂直手前側という意味です。
説明が長くなりましたが、両辺について\bm{r}との外積を取り、
回転成分のみを取り出します。
\bm{r} \times m \bm{r}''=\bm{r} \times \bm{F}このときの左辺は
\begin{align*}
\bm{r} \times m \bm{r}''=&\frac{d}{dt}(\bm{r} \times m\bm{r}')-\bm{r}'\times m\bm{r}'\\
=&\frac{d}{dt}(\bm{r} \times m\bm{r}')
\end{align*}と変形できます。
ここでは(a b)'=a'b+ab'の公式が外積にも適用できることと、
平行な2つのベクトルの外積が0であることを利用しています。
これより
\frac{d}{dt}(\bm{r} \times m\bm{r}')=\bm{r} \times \bm{F}となりますが、ここで左辺の\bm{r}'を\bm{r}に垂直な成分\bm{r}'_vと、平行な成分\bm{r}'_pに分けます。
\frac{d}{dt}(\bm{r} \times m (\bm{r}'_v+\bm{r}'_p))=\bm{r} \times \bm{F}外積は分配法則(\bm{a}\times ( \bm{b} + \bm{c}) = \bm{a} \times \bm{b} + \bm{a} \times \bm{c} )が成り立つので、
\frac{d}{dt}(\bm{r} \times m \bm{r}'_v+\bm{r} \times m\bm{r}'_p)=\bm{r} \times \bm{F}となります。このなかで平行なベクトルの外積は0(\bm{r} \times \bm{r}'_p=0)になるので、
\frac{d}{dt}(\bm{r} \times m \bm{r}'_v)=\bm{r} \times \bm{F}となります。
更に\bm{r}'_vについて考えていきます。
円運動している物体の速度を考えると、下図のように角速度\omegaを用いて
\bm{v}=\bm{r'}=\bm{\omega} \times \bm{r}と表せます。
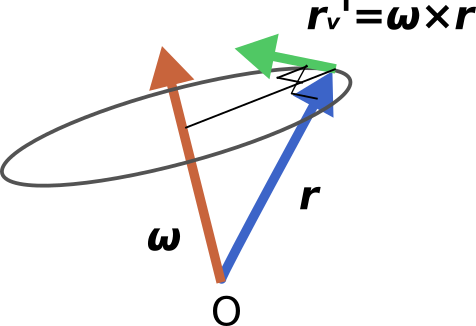
ただし円運動の速度ベクトルは回転半径に垂直である必要がありますが、
\bm{r}'_vは\bm{r}と垂直なので、
上図のようなベクトル\bm{\omega}を定義することができます。
また\bm{r}'は\bm{r}の時間微分なので速度を表しており、
角速度\bm{\omega}の物理的意味も一致していることが分かると思います。
ただし\bm{r}は円運動をしているとは限らないため、
\bm{\omega}は時間ごとに向きや大きさが変化する場合があることに注意してください。
これを用いて式を書き直すと
\begin{equation}
\frac{d}{dt}(\bm{r} \times m( \bm{\omega} \times \bm{r}))=\bm{r} \times \bm{F}
\end{equation}となります。\bm{\omega}は角速度ベクトルです。
ここで、外積には結合法則が成り立たない( (\bm{a} \times \bm{b}) \times \bm{c} \neq \bm{a} \times (\bm{b} \times \bm{c}) )ので、
\bm{\omega} \times \bm{r}を先に計算しなければならないことに注意してください。
この式は、角運動量L、トルクTを
\begin{align*}
角運動量~~\bm{L}=&\bm{r} \times m( \bm{\omega} \times \bm{r})\\
トルク~~\bm{T}=&\bm{r} \times \bm{F}
\end{align*}とすることで
\begin{equation}
\frac{d}{dt}\bm{L}=\bm{T}
\end{equation}と書き表せます。
トルクTは距離×力(垂直成分)であり、皆さんも馴染みがあるのではないかと思います。
角運動量Lは、\bm{\omega} \times \bm{r}が物体の回転方向の速度になるので、
運動量m\bm{v}に距離を掛けた(外積した)ものになっています。
こちらの式(2)が回転運動の基本的な運動方程式となります。
回転運動の運動方程式が示していること
式(2)は角運動量の変化が作用するトルクに等しいという式ですので、
外力等によるトルクが作用していない場合、物体の角運動量は変化しないということを示しています。
このことから式(2)を角運動量保存の式と呼びます。
これは回転運動の法則を表すとても便利で重要な式ですが、
一方でこれは質点運動の特徴の一部を表しているだけの式であることにも注意
しなければいけません。
この式が示しているのは、ある原点をとり、物体の速度の接線方向成分を考えると、
物体に作用する原点周りのトルクと関係性があるということです。
この式を回転する物体に適用することで様々なことが分かりますが、
この式自体が回転運動を示しているわけではないということに注意してください。
例えば物体が円運動を行うためには初速\bm{\omega} \times \bm{r}を持ち、
かつ原点向きの向心力m\bm{\omega} \times (\bm{\omega} \times \bm{r})が作用している必要があります。
ただしこのときの向心力が原点を向いている場合、回転半径と平行になり
トルクを発生させないため、式(2)で考慮することはできません。
この物体にトルクTが作用したときの角運動量の変化(角速度ではなく)は式(2)から求められます。
回転半径rが一定などの条件であれば更にそこから角速度\bm{\omega}の変化を求めることができます。
このように、式(2)は回転運動においてとても重要な\bm{\omega}というパラメータを
表現することができますが、この式を満たせば回転運動をするというものではありません。
もう一つ、この式から得られるのは角速度\bm{\omega}であって角度\bm{\theta}ではないことにも注意してください。
もちろん\bm{\omega}=\bm{\theta}'として\bm{\theta}を定義することはできますが、
これには物理的意味がありません。
物体の速度は\bm{v}=\bm{\omega} \times \bm{r}ですが、物体の位置は\bm{r}そのものであり、
\bm{\theta}の介在する余地がありません。
また、\bm{\theta}が初期位置\bm{r}_0に対する回転を示しているかというとそんなこともありません。
例として\bm{\omega}(t)を0\leq t<5まではx軸の向きに大きさ\pi/10、
5 \leq t <10ではy軸の向きに大きさ\pi/10となる場合を考えます。
これを積分して\bm{\theta}を求めると、
\bm{\theta} = (\frac{\pi}{2},\frac{\pi}{2},0)となることがすぐに分かります。
これは前編の記事で説明した、傾きをどのように表すかという説明における
③のベクトルと一致します。
一方で今回設定した\bm{\omega}(t)が実際に表している運動は、①の場合における図の1段目です。
このように今回紹介した式を用いても\bm{\theta}を表現することはできません。
\bm{\theta}は得られた\bm{\omega}などを用いて、
扱う問題の条件や角度の定義等と合わせて初めて求められるようになります。
剛体の回転運動
ここまで質点の回転運動を説明してきましたが、
元々私たちが知りたかったのは物体の傾きです。
物体が傾くためには、物体が点ではなく形状を持っている必要があります。
ここからはある形状の剛体について、これまで求めた運動方程式を用いて、
その物体の傾きを考えていきます。
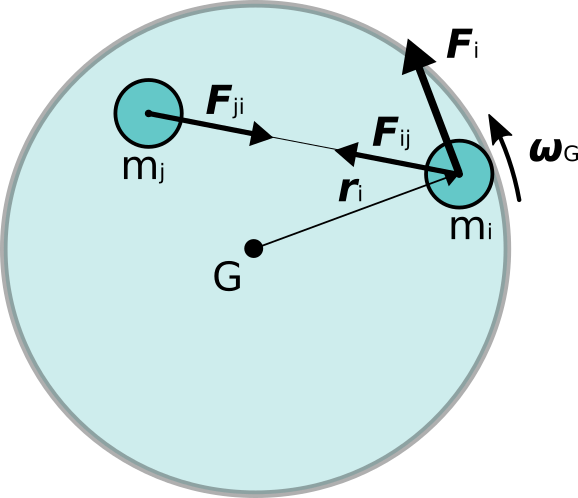
上図のように\bm{\omega}_Gで回転している物体を、それを構成する小さな各部分iに分けて考えます。
物体の形状は何でも良いですが、図では球(または円盤)を描いてあります。
物体の一部であるiの質量はm_iで、重心を原点とした位置は\bm{r}_iであり、
iに作用する外力を\bm{F}_i、物体の他の一部であるjから受ける力を\bm{F}_ijとします。
作用反作用の法則から、iはjに\bm{F}_{ji}=-\bm{F}_{ij}の力を作用させます。
重心回りの回転を考えると、式(2)より
\frac{d}{dt}(\bm{r}_i \times m_i( \bm{\omega}_G \times \bm{r}_i))=\bm{r}_i \times (\bm{F}_i+\bm{F}_{ij})が得られます。
これは物体のすべての部分に成り立つので、これらについて和をとります。
\begin{align}
\sum_i\frac{d}{dt}(\bm{r}_i \times m_i( \bm{\omega}_G \times \bm{r}_i))
=&\sum_i(\bm{r}_i \times (\bm{F}_i+\bm{F}_{ij}))\\
\frac{d}{dt}\sum_i(m_i\bm{r}_i \times ( \bm{\omega}_G \times \bm{r}_i))
=&\sum_i (\bm{r}_i \times \bm{F}_i)+\sum_i(\bm{r}_i \times \bm{F}_{ij})\\
\end{align}この左辺の中の \bm{r}_i \times ( \bm{\omega}_G \times \bm{r}_i) について、
具体的な計算をしていきます。
外積は成分による演算が可能で、\bm{a}=(a_1,a_2,a_3)、\bm{b}=(b_1,b_2,b_3)とすると
\bm{a} \times \bm{b}=(a_2b_3-a_3b_2,a_3b_1-a_1b_3,a_2b_1-a_1b_2)となります。
ここで重心回りにG-\xi \eta \zeta座標系を取り、\bm{r}_i、\bm{\omega}_Gを
\begin{align*}
\bm{r}_i=&(\xi_i,\eta_i,\zeta_i)\\
\bm{\omega}_G=&(\omega_\xi,\omega_\eta,\omega_\zeta) \\
\end{align*}とすると、
\begin{align*}
\bm{\omega}_G \times \bm{r}_i =
&(\omega_\eta \zeta _i -\omega_\zeta\eta _i, \omega_\zeta \xi_i-\omega_\xi \zeta_i, \omega_\xi \eta_i-\omega_\eta \xi_i) \\~\\
\bm{r}_i \times (\bm{\omega}_G \times \bm{r}_i ) =
&(\eta_i( \omega_\xi\eta_i-\omega_\eta\xi_i)-\zeta_i(\omega_\zeta\xi_i-\omega_\xi \zeta_i),\\
&~\zeta_i(\omega_\eta\zeta_i-\omega_\zeta\eta_i)-\xi_i(\omega_\xi\eta_i-\omega_\eta\xi_i),\\
&~\xi_i(\omega_\zeta\xi_i-\omega_\xi \zeta_i)-\eta_i(\omega_\eta\zeta_i-\omega_\zeta\eta_i))\\
=&((\eta_i ^2+\zeta_i ^2)\omega_\xi-\eta_i\xi_i\omega_\eta-\zeta_i\xi_i\omega_\zeta,\\
&~-\xi_i\eta_i\omega_\xi+(\zeta_i^2+\xi_i^2)\omega_\eta-\eta_i\zeta_i\omega_\zeta,\\
&~-\zeta_i\xi_i\omega_\xi-\eta_i\zeta_i\omega_\eta+(\xi_i^2+\eta_i^2)\omega_\zeta)\\~\\
\sum_i(m_i\bm{r}_i \times (\bm{\omega}_G \times \bm{r}_i ))
=&(\omega_\xi\sum_i m_i(\eta_i ^2+\zeta_i ^2)-\omega_\eta\sum_i m_i\eta_i\xi_i-\omega_\zeta\sum_i m_i\zeta_i\xi_i,\\
&~-\omega_\xi\sum_i m_i\xi_i\eta_i+\omega_\eta\sum_i m_i(\zeta_i^2+\xi_i^2)-\omega_\zeta\sum_i m_i\eta_i\zeta_i,\\
&~-\omega_\xi\sum_i m_i\zeta_i\xi_i-\omega_\eta\sum_i m_i\eta_i\zeta_i+\omega_\zeta\sum_i m_i(\xi_i^2+\eta_i^2))\\
=&\bm{I}_G\bm{\omega}
\end{align*}ここで、\bm{I}_Gは慣性テンソルと呼ばれ
\begin{equation}
\bm{I}_G=\begin{pmatrix}
\sum_i m_i(\eta_i ^2+\zeta_i ^2)&-\sum_i m_i\eta_i\xi_i&-\sum_i m_i\zeta_i\xi_i\\
-\sum_i m_i\xi_i\eta_i&\sum_i m_i(\zeta_i^2+\xi_i^2)&-\sum_i m_i\eta_i\zeta_i\\
-\sum_i m_i\zeta_i\xi_i&-\sum_i m_i\eta_i\zeta_i&\sum_i m_i(\xi_i^2+\eta_i^2)\\\end{pmatrix}\\
\end{equation}
となります。また、ここまで行ベクトルと列ベクトルの区別をしていませんでしたが、
ここで\bm{\omega}は列ベクトルで
\bm{\omega}=
\begin{pmatrix}
\omega_\xi\\
\omega_\eta\\
\omega_\zeta
\end{pmatrix}となります。
式(5)は、分割を無限に小さくすることでm_i \to dmとして積分で表すこともできます。
\begin{equation}
\bm{I}_G=\begin{pmatrix}
\int(\eta ^2+\zeta ^2)dm&-\int \eta\xi dm&-\int\zeta\xi dm\\
-\int \xi\eta dm&\int(\zeta^2+\xi^2)dm&-\int \eta\zeta dm\\
-\int \zeta \xi dm&-\int \eta\zeta dm&\int (\xi^2+\eta^2)dm\\\end{pmatrix}\\
\end{equation}また、これらの結果と式(2)より
\bm{L}_G=\begin{pmatrix}
L_\xi\\
L_\eta\\
L_\zeta
\end{pmatrix}
=\bm{I}_G\bm{\omega}_Gであることが分かります。
ここまでの計算でG-xyz座標ではなくG-\xi\eta\zeta座標を使用したのは、
この慣性テンソル\bm{I}_Gが全体座標の向きに依らない
任意の向きに決めることができることを示したかったからです。
慣性テンソルの対角成分は、\eta^2+\zeta^2=r_\xi^2 (r_\xi:\xi軸からの距離)なので、
各軸に関して前編で説明した慣性モーメントと同じになっています。
こちらも慣性モーメントと呼ばれます。
それに対して非対角成分のことを慣性乗積と呼びます。
慣性乗積の意味
さて、急に慣性乗積というものが出てきましたが、
これは2次元平面で回転運動を扱っていたときにはなかった概念です。
3次元空間で回転運動を扱う場合の質量に相当するものが慣性テンソルで、
その非対角成分が慣性乗積です、と言ってしまえばその通りではありますが、
慣性モーメントが回転運動の質量としての意味を持っているのに対し、
慣性乗積がなぜ存在し、何を意味しているのかがすぐにピンとこないと思います。
(2次元平面での回転では、なくても成立していたので…)
もちろん計算をしていくと現れるので必要な要素ですし、
そういうものだ、で済む方もいると思いますが、
ここからは更に慣性乗積の表すものについて考え、理解の足しにしたいと思います。
ここで一旦質点の回転運動に戻り、角運動量がをもう少し詳しく見ていきましょう。
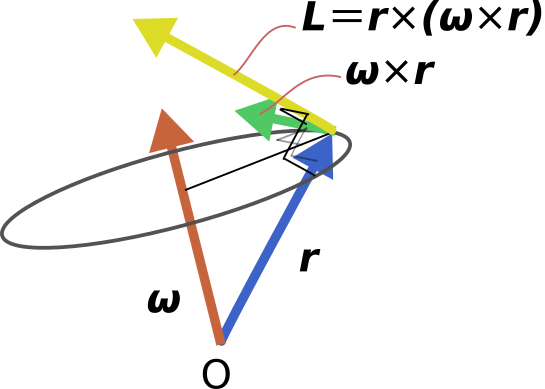
原点から見て位置\bm{r}にある物体の角運動量は上図中\bm{L}の様になります。
\bm{\omega} \times \bm{r}は回転軸\bm{\omega}と垂直な平面上に存在していますが、
\bm{r}は必ずしもその同一平面上にないため、角運動量\bm{L}=\bm{r}\times (\bm{\omega} \times \bm{r})は回転軸\bm{\omega}と角度を持つことになります。
このように3次元空間では回転軸\bm{\omega}と位置\bm{r}が垂直とは限らないため、
回転軸周りに回転させても角運動量が回転軸と平行ではなくなります。
この回転軸と平行でない成分を表すのが慣性乗積です。
なぜ平行でない成分が重要かというと、角運動量\bm{L}の方向は
\bm{r}がの変化とともに変化するためです。
先ほどの図を\bm{\omega}と平行な向きに見てみると下図のようになります。
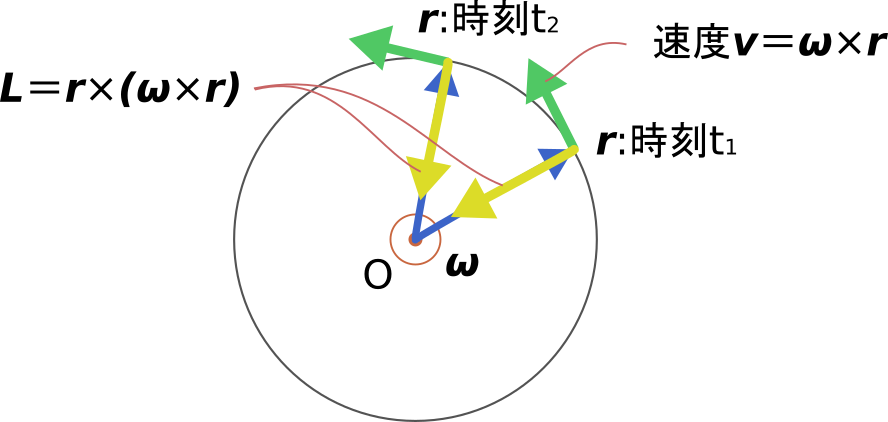
見てわかる通り、角運動量は\bm{L}は\bm{r}と一緒に回転し、
その方向を変化させます。
そして角運動量\bm{L}が時間変化するということはトルク\bm{T}が
作用するということになります。
今回のような円運動する例でいえば、このトルク\bm{T}は向心力によるトルクです。
向心力の向きが原点とずれていますので、原点から見ると向心力となる力は
トルクとして作用していることになりますし、逆にそのようなトルク(向心力)がなければ
回転運動にはなりませんよ、ということを表しています。
このような角運動量の変化をなくすためには、
角運動量が回転軸に平行(=慣性乗積が0)である必要があります。
慣性乗積と慣性主軸
慣性乗積とは角運動量の、回転軸と平行でない成分に相当するものですが、
これは位置\bm{r}が回転軸位置\bm{\omega}と垂直でなければ必ず発生します。
つまり、これまで2次元平面での回転を扱う場合には位置位置\bm{r}が必ず
位置\bm{\omega}と垂直であったため、慣性乗積を意識せずに
慣性モーメントのみを考えて回転を取り扱うことができたということです。
しかし、3次元空間での回転を考える場合には物体は3次元的に質点が分布しており、
それぞれの質点について角運動量を考えた場合には、ほぼ確実に回転軸\bm{\omega}に
平行でない成分が現れます。
これらをすべて足していったものが物体の慣性乗積-\int\eta\xi dmとなりますが、
実はこれらの成分は座標系G-\xi \eta \zetaの向きを適切に選ぶことで、
ちょうど打ち消しあって0となる場合が存在しています。
しかもこのような、ちょうど打ち消しあって慣性乗積が0となる方向は、
3方向存在し、それぞれが互いに直角となります。
つまり、座標系G-\xi \eta \zetaの各軸を上記のような方向と一致させれば、
そのときの慣性テンソルI_{p,\xi\eta\zeta}の慣性乗積はすべて0ということになります。
このような方向を慣性主軸と呼びます。
慣性主軸方向に座標系G-\xi \eta \zetaを取ると角運動量\bm{L}は以下のような簡単な式になるため、扱いが非常に良くなります。
\bm{L}=\bm{I}_p \omega=
\begin{pmatrix}
I_\xi & 0 &0\\
0&I_\eta&0\\
0&0&I_\zeta
\end{pmatrix}
\begin{pmatrix}
\omega _\xi\\ \omega _\eta \\ \omega _\zeta
\end{pmatrix}
=\begin{pmatrix}
I_\xi\omega _\xi \\ I_\eta \omega _\eta \\ I_\zeta\omega _\zeta
\end{pmatrix}
また、慣性主軸は単に扱いが良くなるだけではなく、物理的にも重要な意味を持ちます。
慣性主軸と回転軸が一致しない場合
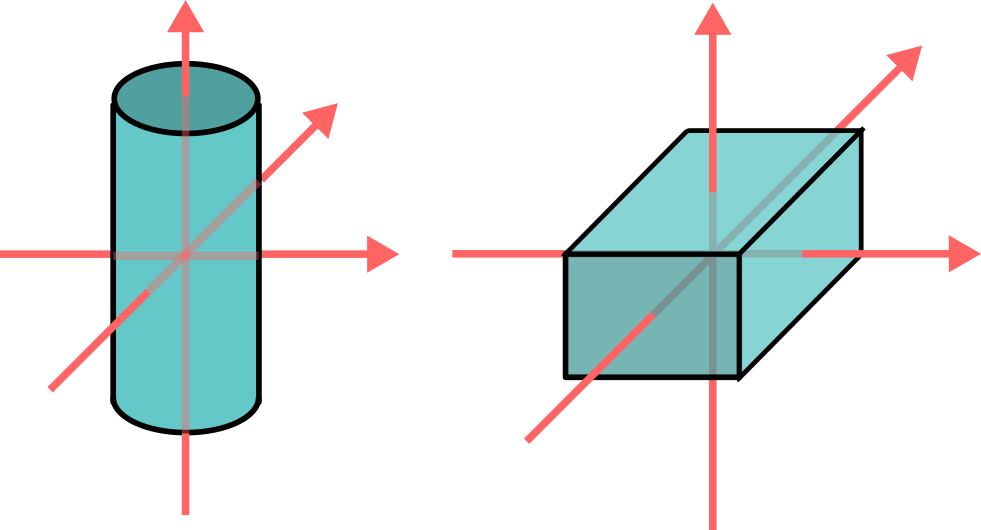
一般的な形状の慣性主軸は上図の様に直感的に回転しやすそうな方向になっています。
これは実際に慣性主軸方向の回転が安定するので、
経験上そのような回転を見る機会がよくあるためだと思います。
当然、一般的な機械では慣性主軸方向に物体を回転させる場合がほとんどです。
しかし、いくら部品を精密に作ったとしても、現実の物体には重さや形状の偏りが
わずかに存在し、慣性主軸と回転軸が厳密に一致しないという場合があります。
このような場合に、どのような現象が起きるか見てみましょう。
単純な1軸の回転軸を持つ機械の回転として角速度\bm{\omega}を
\bm{\omega}=\begin{pmatrix}0\\0\\\omega\end{pmatrix}とします。
今回考えるのは慣性主軸と回転軸が一致していない場合なので、慣性テンソル\bm{I}_pは
\bm{I}_p=
\begin{pmatrix}
I_x&I_{xy}&I_{zx}\\
I_{xy}&I_y&I_{yz}\\
I_{zx}&I_{yz}&I_z
\end{pmatrix}\\~~\\
I_{xy} \neq 0,I_{yz} \neq 0,I_{zx}\neq 0となります。
この結果、角運動量\bm{L}は
\bm{L}=\bm{I}_p\bm{\omega}=
\begin{pmatrix}
I_{zx} \omega\\I_{yz} \omega\\I_z \omega
\end{pmatrix}となり、z軸周り以外の成分が現れます。
トルク\bm{T}は角運動量\bm{L}の時間微分なので、
\omegaが一定であれば0なのではないかと思う方もいるかもしれません。
しかし、z軸周りの回転でz軸と平行でない成分があれば、上でも示したような振れ回りを起こすことになります。

これは各軸に関する慣性テンソルが変化しているために起きる現象です。
この場合で考えているのは慣性テンソルは周囲から見た固定座標G-xyzについての
ものなので、実は物体が回転すると慣性テンソル\bm{I}_pも回転に合わせて変化します。
z軸周りに回転しているのでI_{zx}、I_{yz}、I_zのなかで、I_zのみI'_z=0となり、
他は時間とともに変化することになります。
結果として
\bm{T}=\bm{L}'=
\begin{pmatrix}
I'_{zx} \omega\\I'_{yz} \omega\\0
\end{pmatrix}
というトルクが作用することになります。
これは逆に言えば、回転させるためにはこのような力が作用しなければならないということです。
通常機械の回転体は軸受等で回転軸を固定しているので、
このようなトルクが軸受から回転体に作用し、軸受はその反作用を受けることになります。
この結果、軸受に対して荷重が掛かることで場合によっては軸受寿命が悪化し、
周期的な振れ回り力(=振動)を軸受を支える周囲のケーシングに伝えることになります。
物体の慣性主軸が回転軸と一致している場合には回転軸周り以外のトルクが
不要(=安定)となるので、基本的に回転体は慣性主軸と回転軸が一致するように
運動することになります。
これは以前の記事で紹介したジェフコットロータの、自動調心作用によく似ています。
しかし、ジェフコットロータで紹介した自動調心作用が共振周波数を超えて高速回転する場合に
発生するのに対し、今回の回転軸と慣性主軸が一致しようとする作用は回転した時点で
始まります。
このような点も実は変位と傾きの運動で異なっており、変位と傾きは変数が置き換わっただけで
同じものだと考えていると間違いにつながるので注意してください。
また今回、重心を回転中心とした座標系G-\xi \eta \zetaを用いており、
各書籍等でも慣性テンソルを重心周りで考えている場合がほとんどなので、
慣性主軸は重心周りにしか存在しないと思っている方もいると思います。
これについて末尾のおまけで簡単な検証をしていますので、興味がある方は見てみてください。
重心周りの回転とオイラーの運動方程式
さて、ここまで重心周りの座標系G-\xi\eta\zetaについて話をしてきましたが、
重心周りの座標系を考える利点について説明をしておきます。
回転運動方程式の弱点
回転の運動方程式(2)の弱点はそれ単体で運動のすべてを記述できないことだと思います。
再度回転の運動方程式を見直してみると、回転の運動方程式は
\begin{align*}
\frac{d}{dt}(\bm{r} \times m( \bm{\omega} \times \bm{r}))&=\bm{r} \times \bm{F}\\
\end{align*}
で表されますが、この式はモーメントの腕\bm{r}に対して平行な方向の運動を
完全に考慮することができません。
(当然平行であっても力が働けば位置\bm{r}は変化する可能性がありますが、
この方程式では力のモーメントが0なので何も見えない状態になっています。)
また、この運動方程式には変数\bm{r}、\bm{\omega}が現れます。ここで、
\bm{r}'_v=\bm{\omega} \times \bm{r}
なので、\bm{\omega}は\bm{r}とその微分\bm{r}'を求めれば
求められることになりますが、これは単純に求めるべき変数を1つ増やしているだけとも
言えます。
これらのことから、この回転に関する運動方程式は、元々物体の運動を完全に記述していた
運動方程式を変形して回転速度\bm{\omega}を表現する代わりに多くの利便性を失っています。
重心周りの回転を考えることで、これらの弱点を上手く解消することができます。
重心周りの回転運動の考え方とメリット
物体の重心について回転を考えたとき、位置\bm{r}と速度\bm{r}'は
\bm{r}=\bm{r}_G+\hat{\bm{r}}\\
\bm{r}'=\bm{r}'_G+\hat{\bm{\omega}}\times \hat{\bm{r}}となります。
ここで\bm{r}_Gは重心の位置、
\bm{\omega}_Gは重心の回転速度、
\hat{\bm{\omega}}は重心周りの回転速度で、物体中のすべての質点で同じ値となります。
(上での説明から若干記号が変化していますが、許してください。)
これを用いて原点周りの角運動量\bm{L}を考えると
\begin{align*}
\bm{L}=&\int\bm{r} \times\bm{r}'dm\\
=&\int\{(\bm{r}_G+\hat{\bm{r}}) \times (\bm{r}'_G+\hat{\bm{\omega}}\times \hat{\bm{r}})\}dm\\
=&\int(\bm{r}_G \times\bm{r}'_G)dm
+\int(\bm{r}_G \times(\hat{\bm{\omega}} \times \hat{\bm{r}}))dm
+\int(\hat{\bm{r}} \times\bm{r}'_G)dm
+\int(\hat{\bm{r}} \times(\hat{\bm{\omega}} \times \hat{\bm{r}}))dm\\
=&M\bm{r}_G \times\bm{r}'_G+0+0+\int(\hat{\bm{r}} \times(\hat{\bm{\omega}} \times \hat{\bm{r}}))dm\\
=&\bm{L}_G+\hat{\bm{L}}
\end{align*}となります。
ここで\bm{r}_G、\hat{\bm{\omega}}、\bm{r}'_Gはすべての質点に対して一定なので
重心の特性である\int \bm{r}dm =0を用いて3行目第2項、第3項=0としています。
つまり系全体の角運動量は、原点周りの重心についての角運動量と、
重心周りの物体の角運動量を別々に考えて足せばよいということになります。
これが重心周りの回転運動を考える最大の利点となります。
重心の運動と角運動量は基本的な運動方程式から\bm{r}、\bm{r}'を求めることで
導出することができます。
また、重心周りの運動については剛体であれば各質点への距離|\hat{\bm{r}_i}|が一定なので、
回転方向の運動のみ(=角運動量のみ)を考えれば十分です。
重心周りの角運動量は慣性テンソル\bm{I}_pと角速度\bm{\hat{\omega}}で表現できることは既に説明しましたが、剛体の慣性テンソルは物体の向きに対して一定なので、\bm{\hat{\omega}}のみを考えるだけで良くなります。
(ただしこれらの角運動量に関する特徴は重心周りでなくても剛体であれば同じなので、
厳密には重心周りである利点ではありません。)
オイラーの運動方程式
重心周りの回転運動は回転軸と慣性主軸の方向が一致していれば簡単に書き表すことができます。
しかし、3次元空間での回転を考えるとき、例えばx軸周り、y軸周りの回転を
それぞれに考えるような場合には回転軸と慣性主軸の方向を一致させることはかなり難しいです。
このような場合では、初期位置でx軸、y軸がそれぞれ慣性主軸と一致していたとしても、
x軸に回転運動した時点でy軸と慣性主軸は一致しなくなっています。
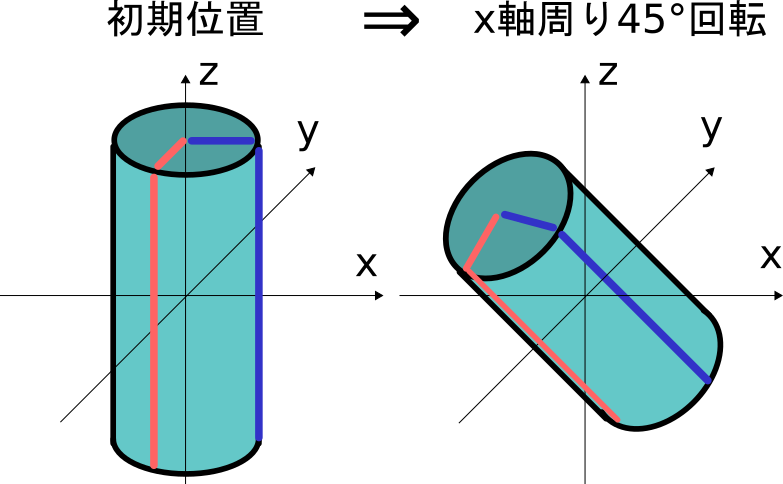
このようなことから、3次元空間で各軸についてそれぞれ回転運動を考える場合、
回転運動に合わせて各軸時間における慣性テンソルを計算する必要がありますが、
これはとても大変です。
そこで3次元空間の各軸について回転をそれぞれ考える場合、
座標系を物体側に固定するという方法がとられる場合があります。
座標系G-\xi\eta\zetaが物体に固定されているので、
物体が剛体であれば座標系G-\xi\eta\zetaについての慣性テンソルは一定となります。
とは言え、これだけで簡単にめでたしめでたし、というわけではなく、
座標系自体が回転することになるので、しっかりと座標変換を行う必要があります。
実際に座標変換を考えてみましょう。
座標系G-\xi\eta\zetaにおける単位ベクトルを座標系\bm{i}、\bm{j}、\bm{k}とします。
座標系は角速度\bm{\omega}=(\omega_\xi,\omega_\eta,\omega_\zeta)で回転しています。
座標系G-\xi\eta\zeta周りの角運動量\hat{\bm{L}}は各成分を用いて
\hat{\bm{L}}=L_\xi \bm{i}+L_\eta \bm{j}+L_\zeta \bm{k}と表されます。こちらを微分して
\hat{\bm{L}}'=L'_\xi \bm{i}+L'_\eta \bm{j}+L'_\zeta \bm{k}+L_\xi \bm{i}'+L_\eta \bm{j}'+L_\zeta \bm{k}'ここで、各軸は\bm{\omega}=(\omega_\xi,\omega_\eta,\omega_\zeta)で回転しているので、これまで何度も使用してきた
\begin{align*}
\bm{r}'=&\bm{\omega} \times \bm{r}\\
\end{align*}
と外積の成分表示を用いることで
\begin{align*}
\bm{i}'=&\bm{\omega} \times \bm{i}\\
=&(\omega_\xi,\omega_\eta,\omega_\zeta) \times (1,0,0)\\
=&\omega_\zeta \bm{j}-\omega_\eta\bm{k}\\~~\\
\bm{j}'=&\bm{\omega} \times \bm{j}\\
=&(\omega_\xi,\omega_\eta,\omega_\zeta) \times (0,1,0)\\
=&\omega_\xi \bm{k}-\omega_\zeta\bm{i}\\~~\\
\bm{k}'=&\bm{\omega} \times \bm{k}\\
=&(\omega_\xi,\omega_\eta,\omega_\zeta) \times (0,0,1)\\
=&\omega_\eta \bm{i}-\omega_\xi\bm{j}\\~~\\
\end{align*}3次元ベクトルの外積の成分表示は
(a_1,a_2,a_3)\times(b_1,b_2,b_)=(a_2b_3-a_3b_2,a_3b_1+a_1b_3,a_1b_2+a_2b_1)
を用いています。この結果を使用して角運動量の微分\hat{\bm{L}}'は
\begin{align*}
\hat{\bm{L}}'=&L'_\xi \bm{i}+L'_\eta \bm{j}+L'_\zeta \bm{k}+L_\xi \bm{i}'+L_\eta \bm{j}'+L_\zeta \bm{k}'\\
=&L'_\xi \bm{i}+L'_\eta \bm{j}+L'_\zeta \bm{k}+L_\xi (\omega_\zeta \bm{j}-\omega_\eta\bm{k})+L_\eta (\omega_\xi \bm{k}-\omega_\zeta\bm{i})+L_\zeta(\omega_\eta \bm{i}-\omega_\xi\bm{j})\\
=&(L'_\xi-L_\eta \omega_\zeta +L_\zeta \omega _\eta)\bm{i}+(L'_\eta-L_\zeta \omega_\xi +L_\xi \omega _\zeta)\bm{j}+(L'_\zeta-L_\xi \omega_\eta +L_\eta \omega _\xi)\bm{k}
\end{align*}となります。ここで重心周りのトルク\hat{\bm{T}}=(T_\xi,T_\eta,T_\zeta)を考えると
\hat{\bm{L}}'=\hat{\bm{T}}なので
\begin{align*}
L'_\xi-L_\eta \omega_\zeta +L_\zeta \omega _\eta=&T_\xi\\
L'_\eta-L_\zeta \omega_\xi +L_\xi \omega _\zeta=&T_\eta\\
L'_\zeta-L_\xi \omega_\eta +L_\eta \omega _\xi=&T_\zeta
\end{align*}という各方向に関する運動方程式が得られます。
更に、座標系G-\xi\eta\zetaの各軸を慣性主軸方向と一致させると、慣性乗積が0になるので
各軸の角運動量は
\begin{align*}
L_\xi =&I_\xi \omega_\xi\\
L_\eta =&I_\eta \omega_\eta\\
L_\zeta =&I_\zeta\omega_\zeta
\end{align*}という風に慣性モーメントI_\xi、I_\eta、I_\zetaのみを用いて簡単に表すことができます。
これを先ほどの式に代入して整理すると
\begin{align*}
I_\xi \omega'_\xi-(I_\eta-I_\zeta)\omega_\eta \omega_\zeta=&T_\xi\\
I_\eta \omega'_\eta-(I_\zeta-I_\xi)\omega_\zeta \omega_\xi=&T_\eta\\
I_\zeta \omega'_\zeta-(I_\xi-I_\eta)\omega_\xi \omega_\eta=&T_\zeta\\
\end{align*}
となります。これをオイラーの運動方程式と言います。
重心の運動は基本的な運動方程式で、重心周りの回転についてはこちらのオイラーの運動方程式を
用いることで物体の並進運動と回転運動の両方を扱うことができます。
ただし、この式に現れる各成分は座標系G-\xi\eta\zetaにおける値であることに注意してください。
例えば静止座標系から見た最終的な位置を求めたい場合などでは、
座標系自体の位置や向きを考慮する必要があります。
オイラーの運動方程式から分かること
この運動方程式から得られる知見として、やはり各回転軸に関する回転運動は
他の回転軸周りの回転の影響を受けることが分かります。
実はこの知見が回転機械の振動を扱う上で重要な要素です。
回転体は文字通り回転していますので、その傾き運動(=回転運動)には
当然回転体がもつ回転の影響を受けます。
これはジャイロ効果などと呼ばれるもので、
独楽などが倒れずに回り続けることの説明などにも使われます。
次回以降、このジャイロ効果が回転体の振動に
どのような影響を与えるのかを説明していきたいと思います。
結言
長くなりましたが、今回は3次元空間での回転運動を扱う方法ついて説明しました。
特に後編では力学分野で回転運動を扱う際に用いられる方法を説明しました。
この結果として物体の運動は、重心の運動と重心周りの回転運動に
分離して考えれば良いことを説明しました。
また、重心周りの回転運動を扱うための手法としてオイラーの運動方程式を導出しました。
説明していく中で、私自身勘違いや曖昧な理解をしていた部分が多々あったため
それらについて私なりに曖昧な部分を無くして書いたつもりですので、
内容は大分長くなってしまいましたが、誰かの参考になれば幸いです。
次回は上でも書いた通り、物体が3次元空間で複数の軸方向に回転した際に現れる
ジャイロ効果が回転体の振動にどのような影響を与えるのかを説明したいと思います。
こちらが最終的に私が説明したかった内容の一つですので、
また内容が長くなるかもしれませんが、回転体振動特有の興味深い現象ですので
是非見てもらえればと思います。
おまけ:重心周りでない系の慣性モーメント・慣性主軸
慣性テンソル\bm{I}_pは式(6)から
\begin{equation*}
\bm{I}_p=\begin{pmatrix}
\int(\eta ^2+\zeta ^2)dm&-\int \eta\xi dm&-\int\zeta\xi dm\\
-\int \xi\eta dm&\int(\zeta^2+\xi^2)dm&-\int \eta\zeta dm\\
-\int \zeta \xi dm&-\int \eta\zeta dm&\int (\xi^2+\eta^2)dm\\\end{pmatrix}\\
\end{equation*}で表されるため、重心を通らない座標系O-\xi \eta \zetaについても定義することができます。
一方で、慣性主軸については多くの書籍で座標系G-\xi \eta \zetaについてのみ語られており、
重心を通る場合にのみ存在すると思っている方もいるのではないかと思います。
しかし、実は慣性主軸の存在を保証する理論の中には、重心に限定する要素は含まれていません。
このことから重心を通らない座標系O-\xi \eta \zetaでも慣性主軸は定義できるはずですが、
私自身あまり自信がなかったので簡単な検証をしてみることにしました。
あまり線形代数が得意ではないので、証明ではなく数値演算による検証となりますが、
興味があれば見てみてください。
今回扱うのは下図のような系です。

この時の\bm{I}_pは
\begin{align*}
\bm{I}_p=&\begin{pmatrix}
\int(y ^2 + z ^2)dm &-\int yxdm &-\int zx dm\\
-\int xy dm&\int(z^2+x^2)dm&-\int yz dm\\
-\int z x dm&-\int yz dm& \int (x^2+y^2)dm\\\end{pmatrix}\\
\end{align*}となります。(ここでのx,y,zは軸方向の意味で、物体の基準点(X,Y,Z)とは違います。)
物体の質量がMで、一様だとすると
dm=\frac{M}{abc}dxdydzとなり、x,y,zはそれぞれ独立なので各成分について積分すると
\begin{align*}
\int (y^2+z^2)dm=&\int(y^2+z^2)\frac{M}{abc}dxdydz\\
=&\frac{M}{abc}\Biggl[x\int(y^2+z^2)dydz\Biggl]_{x= X} ^{x=X+a} =\frac{M}{abc}a\int(y^2+z^2)dydz\\
=&\frac{Ma}{abc}\Biggl[\int(\frac{1}{3}y^3+z^2y)dz\Biggl]_{y=Y}^{y=Y+b}
=\frac{Ma}{abc}\int(\frac{1}{3}(3Y^2b+3Yb^2+b^3)+z^2b)dz\\
=&\frac{Mab}{abc}\Biggl[\frac{1}{3}(3Y^2+3Yb+b^2)z+\frac{1}{3}z^3\Biggl]_{z= Z}^{z=Z+c}\\
=&\frac{Mab}{abc}(\frac{1}{3}(3Y^2+3Yb+b^2)c+\frac{1}{3}(3Z^2c+3Zc^2+c^3))\\
=&M(Y^2+Yb+\frac{b^2}{3}+Z^2+Zc+\frac{c^2}{3})\\~~\\
-\int xydm=&-\int xy\frac{M}{abc}dxdydz\\
=&-\frac{M}{abc}\Biggl[z\int xydxdy\Biggl]_{z= Z} ^{z=Z+c} =-\frac{M}{abc}c\int xydxdy\\
=&-\frac{M}{abc}c\Biggl[\int \frac{1}{2}x^2ydy\Biggl]_{x= X} ^{x=X+a} =-\frac{M}{2abc}c\int (2ax+a^2)ydy\\
=&-\frac{M}{2abc}ca\Biggl[ \frac{1}{2}(2x+a)y^2\Biggl]_{y= Y} ^{y=Y+b} =-\frac{M}{4abc}ca (2x+a)(2by+b^2)\\
=&-\frac{M}{4}(2x+a)(2y+b)
\end{align*}がそれぞれの項について成り立ちます。
このまま計算を続けるのは大変なので、今回は具体的な数値を入れて計算をしていきます。
(X,Y,Z)=(1,2,3)、(a,b,c)=(18,12,6)として各項を計算すると
\begin{align*}
\bm{I}_p=&\begin{pmatrix}
115 &-80 &-60\\
-80&166&-48\\
-60&-48&203\\\end{pmatrix}\\
\end{align*}この\bm{I}_pの慣性主軸方向の単位ベクトル\bm{i}、\bm{j}、\bm{k}は
\begin{align*}
\bm{i}=&-0.73830306\bm{x}-0.54770434\bm{y}-0.39360964\bm{z}\\
\bm{j}=&-0.65471443\bm{x}+ 0.72218757\bm{y}+0.22314598\bm{z}\\
\bm{k}=&-0.16204197\bm{x}-0.42245127\bm{y}+0.89178323\bm{z}\\
\end{align*}
となります。(\bm{x}、\bm{y}、\bm{z}は座標系O-xyzの単位ベクトルです。)
これは\bm{I}_pの固有ベクトルになります。
まず単位ベクトルであることを確認します。
\begin{align*}
|\bm{i}|=&(-0.73830306 )^2+(-0.54770434)^2+(-0.39360964)^2=1.0\\
|\bm{j}|=&(-0.65471443)^2+(0.72218757)^2+(0.22314598)^2=1.0\\
|\bm{k}|=&(-0.16204197)^2+(-0.42245127)^2+(0.89178323)^2=1.0\\
\end{align*}
プログラムに計算させているので、表示有効桁などの関係で手計算した場合とは
結果が少し異なると思いますが、その場合でも大きさはほぼ1となっているはずです。
次に単位ベクトル\bm{i}、\bm{j}、\bm{k}が直交しているかを調べます。
直交していれば内積が0となるので各単位ベクトルの内積を取ります。
\begin{align*}
\bm{i} \cdot \bm{j}=&-0.5091482726502848\\
=&-0.73830306\times -(0.65471443)+(-0.54770434)\times 0.72218757\\
&~+(-0.39360964)\times 0.22314598\\
=&-1.1102230246251565\times10^{-16}\\
\bm{j} \cdot \bm{k}=&0.0\\
\bm{k} \cdot \bm{i}=&-5.551115123125783\times 10^{-17} \\
\end{align*}
プログラムによる数値計算なので少し誤差が出ていますが、
ほぼ0と見なしてよいと思います。
内積が0なので単位ベクトルが直交していることが分かります。
最後にこの単位ベクトルの向きに回転させたときの角運動量を計算し、
それが回転軸と平行かを見てみます。平行であれば外積が0なので
\begin{align*}
\bm{i}\times\bm{L}_i=&\bm{i}\times(\bm{I}_p\bm{i})=(0.0000000, 0.0000000 -4.4408921\times 10^{-16})\\
\bm{j}\times\bm{L}_j=&\bm{j}\times(\bm{I}_p\bm{j})=(-2.22044605\times 10^{-16} ,0.00000000, 0.00000000)\\
\bm{k}\times\bm{L}_k=&\bm{k}\times(\bm{I}_p\bm{k})=(4.44089210 \times 10^{-16},-2.22044605\times 10^{-16}, 0.00000000)\\
\end{align*}
こちらも少し誤差がありますが、各成分はほぼ0であるといっていいと思います。
(複雑になるので計算内容は省略します。
行列の積を取った後に外積計算をすれば上のような値が得られます。)
外積が0なので各単位ベクトルと、単位ベクトル方向に回転させたときの角運動量は
平行になります。
これらの結果から、3つの軸が直交し、その各軸周りに回転運動させたときに
角運動量が一定となる原点O周りの座標系O-\xi\eta\zetaが存在することが分かります。
(単位ベクトルの大きさは一応計算しましたが、定数倍してもその後の計算が変わらないので
別に必要ありませんでした。)
原点を通る3つの直角な単位ベクトルすべてが、
原点に存在しない物体の重心を通ることはあり得ません。
(ちゃんと証明する場合には重心の位置ベクトル(x+a/2,y+b/2,z+c/2)と各単位ベクトルが
平行ではない(= 外積≠0)であることを示します。)
これは必ずこのような座標系が存在することの証明ではないですが、
慣性主軸は必ずしも重心Gを通る必要はないという反証になります。