さて、前回まで振動学の基本を説明しました。
ここからはこれまでの基本を踏まえて回転機械を扱うための知識について説明していきたいと思います。
これから説明する内容ですが、基本的には理論よりの内容で、
どちらかと言えば「回転体の振動」と言う方が適当な内容になる予定です。
(今更なのでタイトルはこれまで通り回転機械の振動とします。)
回転機械の振動に関する書籍等を見ると、理論から実践まで様々なことについて触れており、
それらをすべて網羅するのは私には難しいかなと思います。
元々この一連の記事を書こうと思った理由の一つとして、回転機械の振動には私が大学でちゃんと
習わなかったような現象が現れ、それを自分なりに理解できたと思ったので、
改めて筋道を立てて説明したいということがあります。
なので回転機械振動特有の現象について、その基本にある理論的な部分を説明する記事に
していきたいと思っています。
回転体の振動の特徴
回転体の振動を運動として(力学的に)考えたとき、
私が考える回転体でない物体の振動との違いは下記の2点だと思っています。
・回転体の持つインバランス自体が加振力になる。
・傾き方向の運動を考えるなければならない場合がある。
これらの2点から回転体の運動にどのような現象が現れるかというと
・回転数を共振周波数を超えて更に上げていくと、振幅が一定値に近づいていく(自動調心作用)
・停止中の共振周波数に対し、回転中の共振周波数が変化する。
というような現象が起きます。
特に自動調心作用については多くの書籍で取り扱っているのに対し、
2番目の回転中の共振周波数については回転体を専門とした書籍にしか
書いてない場合が多く、私も仕事の中で触れるまで知りませんでした。
ここからは、これまで参考にした「機械力学 森北出版 末岡淳男・綾部隆 共著」の他に
「回転機械の振動 実用的振動解析の基本 コロナ社 松下修己 他共著」も
参考にしていきます。
ただしこちらの書籍は、内容はとても有用ですが、解析手法等に重きを置いていますので、
基礎の部分を知りたいという方は別の書籍を探すのが良いかもしれません。
(私自身も他の書籍を買うか考え中です…)
上記書籍で言葉足らずな部分等については私なりに調べたりした内容を書きますので、
間違い等ありましたら指摘していただけるとありがたいです。
2次元空間での振動
これまで説明してきたモデルでは振動の方向が1次元(x方向のみ)でした。
しかし、これから回転体の運動を扱っていく場合、
これを2次元空間以上に拡張する必要になります。
(1次元の直線運動では回転運動を表すことができません。)
そこでまずは、2次元空間での振動について説明したいと思います。
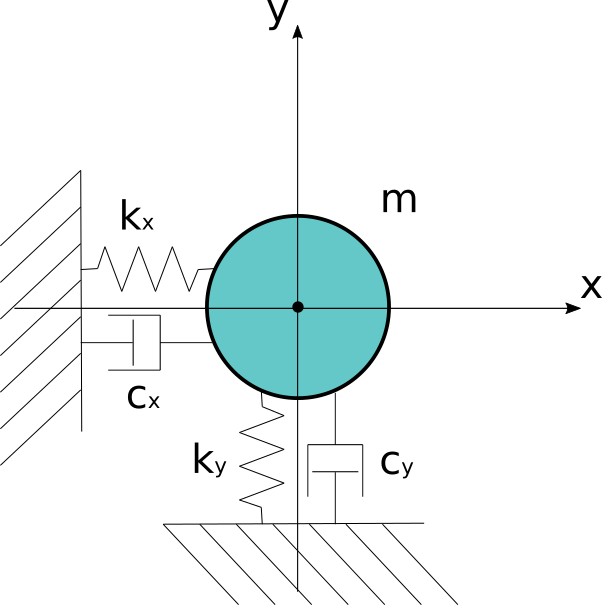
上図のようにx-y空間上で質量mの物体が運動します。
物体は各方向にばねと減衰器でつながれており、
それぞれにばね定数k_x、k_yと粘性減衰係数c_x、c_yを持っています。
このような2次元の運動を場合、素直にx方向とy方向の運動方程式を立てます。
各方向の運動方程式は
x''=-k_x x-c_x x' +F_x^{*}\\
y''=-k_y y-c_y y'+F_y^{*}となります。F_x^{*}、F_y^{*}はそれぞれの方向のばね・減衰以外による外力です。
これは、これまで扱ってきた運動方程式と同じです。
このことから外力がなく、最初にある変位を与えて静かに手を離せば
これまで同様の単振動運動をすることになります。
ただ、これまで扱ってきた運動方程式と違うのは初期にある変位を与えると共に、
それとは別の方向に速度が与えられることです。
これにより物体は円運動、または楕円運動をすることになります。
いずれの場合もx,y方向に運動方程式を立て、それらの関係を見ればどのような運動をしているか
分かります。
極座標系
また、これまで通りx,yを用いて運動を表現するのも、もちろん良いのですが、
回転を扱う場合は半径方向長さrと回転角\thetaを用いた
極座標系を用いる場合が多いです。

極座標系を用いることで半径と回転角の式になるので、
上で説明したような円運動・楕円運動が理解しやすくなります。
(例えば回転角の変化=回転速度ですし、
半径が一定であれば円運動、回転速度に同期した変化があれば楕円運動になります。
減衰がある場合には半径が時間とともに小さくなっていきます。
ばね定数がx,y方向で違う場合にはそれ以外の運動になる場合もあります。)
これらの座標変換をする場合、図中にもある通り各パラメータは以下の様な関係になります。
x=rcos\theta\\ y= rsin\theta
ただし座標変換を行う際には微分などに影響が出る場合があるので、注意が必要です。
今後はその都度、都合の良い座標系で説明する場合があります。
2次元の振動(回転体の場合:ジェフコットロータ)
ではここからは物体が回転している場合を考えてみましょう。
今回扱うのは先ほども示した振動系で、物体が角速度ωで回転している場合です。
このようなモデルで表される有名な振動系として、ジェフコットロータと呼ばれるものがあります。

ジェフコットロータでは、上図のように質量mの薄い円盤の中心を
質量を持たない長棒状のばねで支え、更にその長棒状のばねが両端で
回転可能な様に単純支持されています。
長棒状のばねは通常異方性のないものを考えますので、
どの方向に円盤を変位させてもばね定数はkとなります。
先ほど示したモデルではばねが2つあったのに対し、
今回の図ではばねが1つしかありません。
物理をかじったことがある方であればすぐに分かると思いますが、
一応ばねによる各方向の力の説明をしておきます。

ばねの力は変位の方向と同一直線上に作用するので、上図の様にばねの力の各方向成分は
それぞれの方向に変位を分解して、ばね定数を掛ければ良いことがすぐに分かると思います。
このことから、ジェフコットロータは上で示した2次元振動モデルにおいて
k_x=k_y=k、c_x=c_y=0としたものであることが分かります。
ジェフコットロータの運動方程式
さて、このようなモデルの運動について考えますが、ただ物体回転させただけでは
先ほど示した運動方程式に影響はありません。
ではどのような場合を考えるかというと、
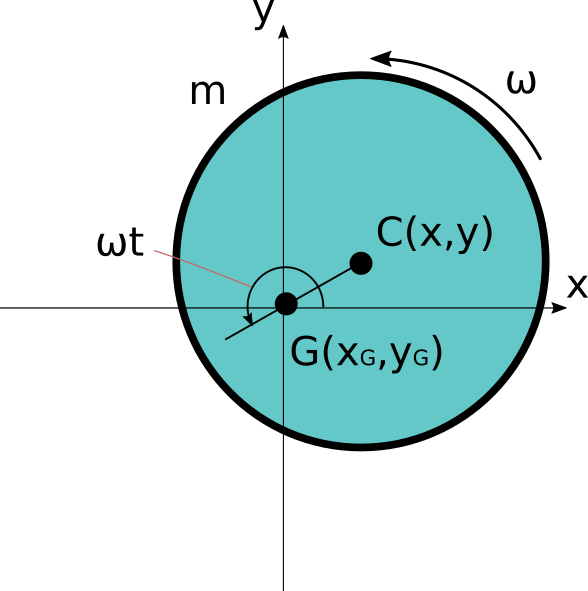
円盤の重心と中心(または回転中心)がずれている場合です。
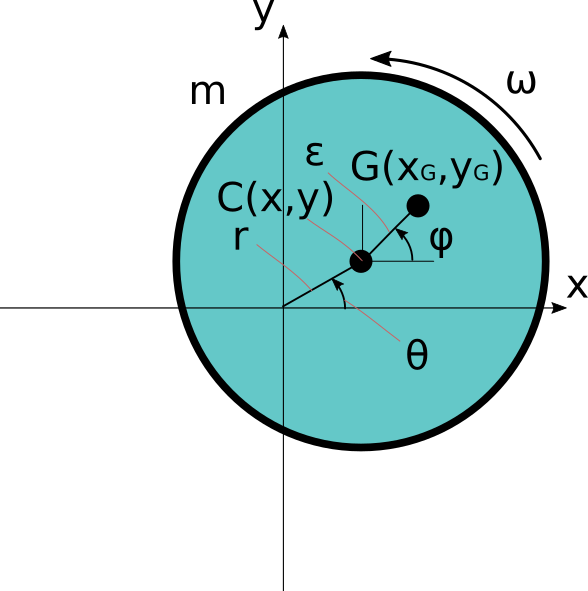
図がごちゃごちゃしていますが、物体の中心をCとして、そこから\varepsilonだけ
離れた位置に物体の重心Gがあります。
物体の中心にはばねが繋がっており、その中心の位置(x,y)を極座標系を用いてr,\thetaで表します。
また物体が回転するので、x-y座標系から見るとCとGの位置は時間により変化します。
これを極座標系を用いて\varepsilon 、\phiで表しています。
時間t=0における\phiを\phi=0とすると
\phi=\omega t
と表されます。
時間の基準t=0となるタイミングや、直交座標系の方向x-yを上手く調整すれば
これは容易に実現できますし、また、以降の説明では時間経過による
過渡的な変化についてはほとんど議論しませんので、これが成り立つとして
話を進めます。
このような中心Cと重心Gがずれた円盤を考えた場合に何が起きるかというと、
遠心力が発生します。
実際に運動方程式を立ててみましょう。
運動方程式は物体の重心について考えますが、ばねは中心につながっているので
\begin{align}
mx_G''&=-kx\\
my_G''&=-ky
\end{align}となります。一見ただの自由振動の運動方程式に見えますが
\begin{align*}
x_G &=x+\varepsilon cos\omega t\\
y_G &=y+\varepsilon sin\omega t
\end{align*}なので、これを式(1)(2)に代入して
\begin{align*}
m(x''-\varepsilon \omega ^2cos\omega t)&=-kx\\
m(y''-\varepsilon \omega ^2sin\omega t)&=-ky
\end{align*}式を整理して
\begin{align}
x''+\omega_n^2x=&\varepsilon \omega ^2 cos\omega t\\
y'' +\omega_n^2y=&\varepsilon \omega^2 sin\omega t\\
\end{align}となり、右辺に外力の項が現れることが分かります。ここで\omega _n =\sqrt{k/m}です。
これらの運動方程式を解く場合、それぞれについて特解を求めても良いのですが、
これらを更にオイラーの公式
e^{i\omega t}=cos\omega t+isin\omega t\\
i^2=-1と
\textbf{\textit{z}}=x+iy\\
\textbf{\textit{z}}''=x''+iy''
を用いて
\begin{align*}
(x''+iy'')+\omega_n^2(x+iy)=&\varepsilon \omega ^2 (cos\omega t+isin\omega t)\\
\textbf{\textit{z}}''+\omega _n ^2\textbf{\textit{z}}=&\varepsilon \omega ^2 e^{i\omega t}\\
\end{align*}と表します。1行目では各辺について 式(3)+i×式(4)としています。
円運動や三角関数の微積分で表される物理現象はこのような表記が可能な場合が多く、
扱いが便利なためよく使われます。
これは線形非同次微分方程式なので、一般解は右辺=0とした線形同次微分方程式の
一般解と特解の和となります。
線形微分方程式の解法は以前書いた番外編の記事を参考にしてください。
回転機械の振動 番外編1. 微分方程式の解法
これらのうち線形同次微分方程式の一般解の部分は下記の様になりますが、
通常であれば減衰して時間とともに0になるため、考えなくても問題ありません。
\textbf{\textit{z}}=C_1e^{i\omega _n t}+C_2e^{-i\omega _n t}ただし、現実世界では減衰がないということはありませんが、今回のモデルでは減衰がなく、
また金属棒をばねとして使用する場合減衰はとても小さくなります。
これらの影響を無視できない問題を扱う場合には一般解の部分にも注意してください。
どちらにしても、一般解の部分には振動特性としての意味が薄いため今回は考えません。
では特解を求めていきます。特解Zを
\textbf{\textit{Z}}=Ze^{i\omega t}とすると、これを運動方程式に代入して
\begin{align*}
-Z\omega^2+Z\omega _n ^2=&\varepsilon \omega ^2\\
(\omega_n ^2- \omega^2)Z=&\varepsilon \omega ^2\\
Z=&\frac{\omega ^2}{\omega _n ^2-\omega ^2}\varepsilon\\
=&\frac{(\frac{\omega}{\omega_n})^2}{1-(\frac{\omega}{\omega_n})^2}\varepsilon
\end{align*}が得られます。これより特解Zは
\textbf{\textit{Z}}=\frac{(\frac{\omega}{\omega_n})^2}{1-(\frac{\omega}{\omega_n})^2}\varepsilon e^{i\omega t}Zの実部がx、虚部がyを表しているので
\begin{align*}
x=&\frac{(\frac{\omega}{\omega_n})^2}{1-(\frac{\omega}{\omega_n})^2}\varepsilon cos\omega t\\
y=&\frac{(\frac{\omega}{\omega_n})^2}{1-(\frac{\omega}{\omega_n})^2}\varepsilon sin\omega t\\~~\\
x_G=&\frac{1}{1-(\frac{\omega}{\omega_n})^2}\varepsilon cos\omega t\\
y_G=&\frac{1}{1-(\frac{\omega}{\omega_n})^2}\varepsilon sin\omega t
\end{align*}となります。
この結果を極座標系の表記で考えると、中心C、重心Gについてそれぞれ
\begin{align*}
r_C=|\frac{(\frac{\omega}{\omega_n})^2}{1-(\frac{\omega}{\omega_n})^2}\varepsilon|\\
r_G=|\frac{1}{1-(\frac{\omega}{\omega_n})^2}\varepsilon|\\~~\\
\omega < \omega_nのとき\\
\theta _C=\theta=\omega t\\
\theta_G=\phi =\omega t\\
\omega > \omega_nのとき\\
\theta _C=\theta=-\omega t\\
\theta_G=\phi =-\omega t
\end{align*}となり、振幅一定、角速度\omegaの円運動であることが分かります。
これらの結果について、まずは振幅r_C、r_Gについて見ていきましょう。
それぞれをグラフに表すと以下の様になります。
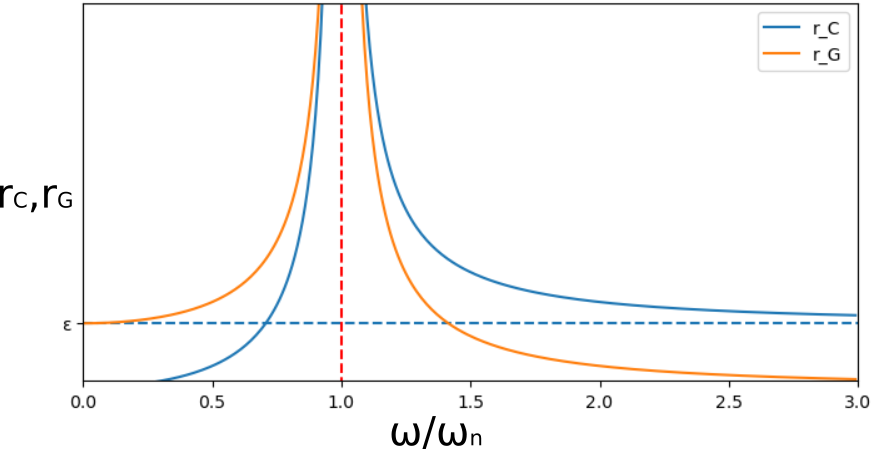
減衰がないので\nu=\omega /\omega_n = 1のとき振幅は無限大になります。
この\omega=\omega_n を危険速度と言います。
現象としては共振と同じと考えてもらってよいと思います。
位相遅れも\omega=\omega_n を境に加振力の方向\omega tを基準として
0 \to \pi に変化しており、これも減衰無しの時の位相と同じになります。
もう一つ特徴的なのが、\omega \to 大のときr_C\to \varepsilon 、r_G \to 0になっていることです。
これはどのような状態か考えてみましょう。
\omega > \omega _n のとき、位相はどちらも\omega < \omega_n のときから反転して一致しています。
またr_C、r_Gの大小関係が逆転して、r_C>r_Gとなります。
これらのことを考慮すると、\omega < \omega_nのときと、\omega >> \omega _nのときで、ジェフコットロータは以下の様な運動をしていることが分かります。
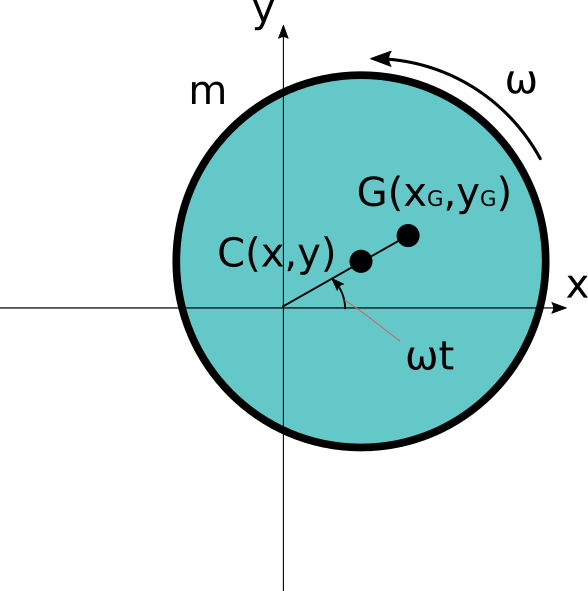
左側が低速(\omega < \omega_n)の時、右側が高速(\omega >> \omega_n)のときです。
振幅のグラフを見てわかる通り、\omega > \omega_nであっても、\omega = \omega_n付近では振幅が大きいですが、\omega >> \omega_nになるとr_G\to 0となります。
つまり、危険速度を通過して更に回転速度\omega が高速になると、
ジェフコットロータは重心を中心とした回転運動に近づいていきます。
これは回転体の自動調心作用と呼ばれ、当然ジェフコットロータ以外でも現れる、
回転体の振動における大きな特徴の一つです。
これをちゃんと理解しおらず、なまじ遠心力について知っていると、
「軸のインバランスによって軸に作用する力は\omega^2で増えていく」といった
勘違いにつながります。
そのような大きな荷重を支えられる軸を設計しようとすれば、
おのずと軸径は太くなり、場合によっては無駄な材料費をかけてしまうことに
なるかもしれません。
また、今回のジェフコットロータでは軸がばねでしたが、
回転体の支えにゴムダンパ等を使用する場合、ゴムダンパの共振周波数よりも
高い回転数で使用している場合がほとんどですので、
ゴムダンパの変位はほぼ偏心量に一致します。
このためゴムダンパが基礎に伝える力はばね定数kが小さいほど小さくなります。
(これは伝達率の部分で説明したのとほぼ同じことです。)
結言
今回はジェフコットロータを例にして回転体の自動調心作用について説明しました。
現実世界では偏心のない回転体などはほぼ存在せず、
工業製品では多くの場合バランス取りをして偏心量を一定値以下に抑えています。
それでもやはり偏心量を0にするというのは難しく、偏心がある回転体を回転させたときに
どのような挙動になるのかは、是非知っておいてもらえればと思います。
次回以降は、回転体の振動におけるもう一つの大きな特徴である、
傾き方向の振動について説明したいと思います。