以前の記事にも書きましたが、ニューラルネットワークの深層化はアイディア自体は昔からあるもので、実際深層化を試みた例はあります。
ただし、深層化したニューラルネットワークを上手く学習する方法が確立されておらず、ニューラルネットワークに対する期待も一時は下がっていました。
ニューラルネットワークを学習する上での問題点は以前の記事に書いた通り主に下記の3点です。
- 勾配消失
- 過学習
- 局所解
また、その問題を上手く回避して学習を行うために用いられる手法として下記の4つを挙げさせてもらいました。(色々調べて1つ手法を追加しました。)
- ReLU (活性化関数)
- 畳み込み層
- Pooling層
- Dropout
- バッチ正規化 (今回追加)
実は、初期のころに深層化ネットワークの学習を成功させた手法はこのいずれでもなく、ネットワークの重み初期値を事前学習により決定するという方法だったようです。
事前学習には同じくニューラルネットワークを用いた、オートエンコーダという手法が使われました。
今日では上に挙げた手法を使うことでこのような事前学習を行わなくても学習が上手くいくようになったため、あまりメジャーな方法ではないようです。
ここでは上に挙げた5つの手法について少し説明していこうと思います。
活性化関数ReLU(Rectified Linear Unit)
ReLUはRectivied Linear Unitの略で、最近の深層学習における活性化関数としてとても良く使われています。
具体的には
として表される関数で、分野等によってはランプ関数などと呼ばれることもあります。
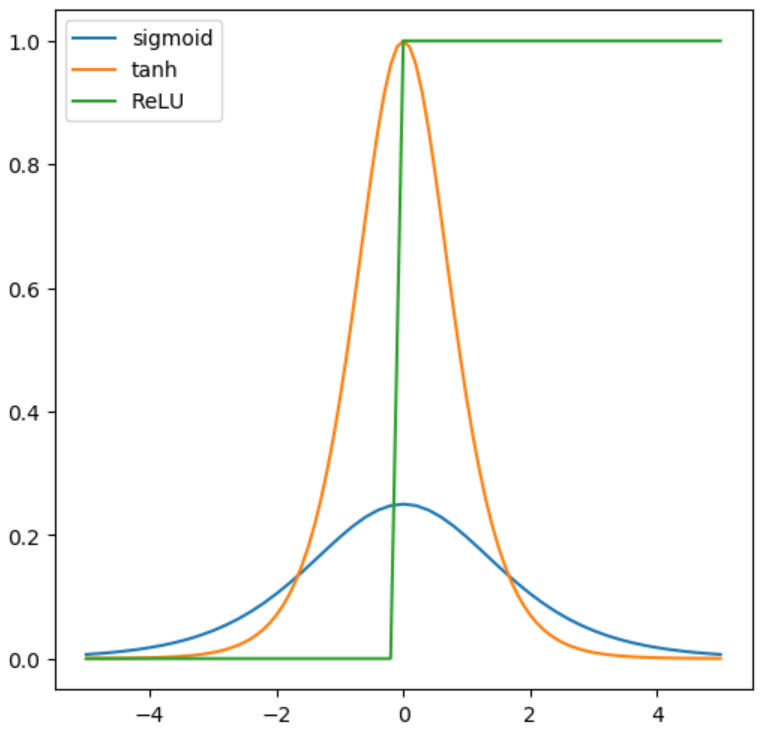
関数の形状は以下の図のようになっています。
(比較のため活性化関数として使用されるSigmoid関数とtanh関数も載せています。)

また、導関数(微分)は下図のようになっています。
ニューラルネットワークでは層から層に順伝播する際に、入力の和を取った後に活性化関数を通します。
誤差を逆伝播する際にはこの活性化関数の微分を掛けたものが誤差として伝播されていくようになっています。
活性化関数の微分が1よりもかなり小さいと、層を遡るごとにこれが何度もかけられていくので、伝播される誤差は急激に小さくなっていきます。これが勾配消失です。(例:3層のネットワークで微分値0.1の場合 0.1×0.1 ×0.1 = 0.001 = 0.1%)
上の図に示した通り、ReLUの微分はx>0では常に1となるので、伝播する誤差が小さくなりにくくなります。
(例:3層のネットワークの場合 1.0×1.0 ×1.0= 1.0 = 100% 上例の1000倍)
ニューラルネットワークは活性化関数と共に進歩してきた、という人もいるくらいに活性化関数は重要な要素です。
ReLUは単純なため計算も簡単で、しかも性能が良いため現在のところ活性化関数のスタンダードになっているようです。
Sigmoid関数やtanh関数が全く使われないかというと、そういう訳ではないですが、中間層で使われることはかなり少なく、多くがネットワーク出力層の値域を限定したい場合に使用されています。
Sigmoid関数の出力は0~1になるので、クラス分類等の確率を示し場合に使用されます。(3クラス以上の場合はsoftmax関数)
tanh関数の出力は-1~1なので、値がある範囲にあってほしい場合に使用されます。これはSigmoid関数でも可能ですが、tanhを使用したほうが広いレンジに分布した良い結果が得られやすいらしいです。
(例えば画像のpixel値:0~255が欲しい場合、(出力+1) ×(255.0/2)とすれば 0~255の範囲の値が得られます。)
畳み込み層
畳み込み層は主に画像認識を行う深層学習に用いられます。
動画に対する深層学習では3次元ベクトル(チャンネルを含まず)に対する畳み込みを行う場合もあるようですが、今回の説明は画像を対象とした2次元の畳み込みについて説明します。
畳み込み演算
畳み込み演算では入力されるベクトル2次元のベクトルに畳み込み呼ばれる操作を行って2次元のベクトルを出力します。
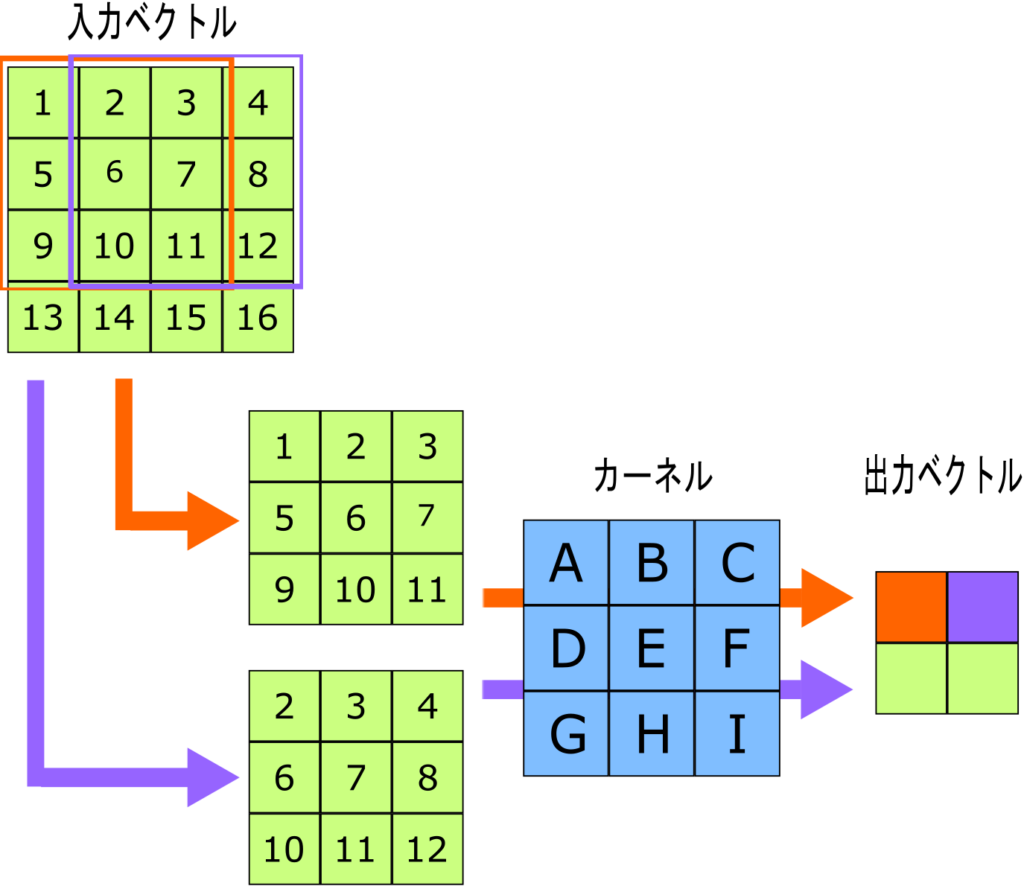
上の図は畳み込み演算の概略を示しています。
入力は4×4のベクトルです。今回は簡単のためチャンネル1個だけの場合ですが、チャンネルが複数ある場合は出力ベクトルを各チャンネルで計算後、足し算します。チャンネルは、例えば画像が白黒であれば1チャンネルですが、RGBのカラーであれば3チャンネルとなります。
演算にはカーネルと呼ばれる2次元のベクトルを用います。(図中の青い2次元ベクトル)
入力ベクトルからカーネルと同サイズの2次元ベクトルを切り出し(図中オレンジの範囲)、カーネルと畳み込み演算を行います。
畳み込み演算は
で計算されます。ただしx_{i,j}、k_{i,j}はそれぞれ入力ベクトルから切り出したベクトル、カーネルを表します。convはスカラーになります。
同様に場所を変えて入力ベクトルからベクトルを切り出していき(図中紫の範囲)、最終的な出力ベクトルを計算します。
今回の例では入力が4×4ベクトルで、カーネルが3×3ベクトルなので、入力ベクトルから切り出せるベクトルは2個(2×2個)になり、出力ベクトルは2×2ベクトルとなります。
カーネルのサイズが1×1ベクトルでなければ、今回のように入力と出力ベクトルのサイズが異なります。
入力と出力のベクトルサイズを合わせたい場合には、パディングと言って入力ベクトルの周囲を拡張して同じ数のベクトルを切り出せるようにします。
畳み込み演算自体は実は画像認識分野では昔から行われてきた手法です。
例えばカーネルとして
というようなカーネルを用いることで、画像中のx方向エッジを検出することができます。(処理後のベクトルを見るとエッジに対応する部分の数字が大きくなります。)
同様に転置したk_yを用いることでy方向のエッジも検出できるので、併せて画像のエッジを検出できます。(2つの平均を取る場合などが多いようです。)
このような演算手法をニューラルネットワークに応用したのが畳み込み層(畳み込みニューラルネットワーク:CNN(Convolutional Neural Network))です。
元々画像認識の分野ではある程度確立された手法ですので、これが良い性能を発揮するというのは納得できることだと思います。
畳み込み層の概略
畳み込み層は畳み込み演算用のカーネルを学習します。一般的に用いられる畳み込み層ではカーネルのサイズを固定にし、カーネルの中身の数値を学習していきます。
畳み込み層は複数のカーネルを持ち、1つのカーネルで計算された出力ベクトルが最終的な出力ベクトルの1チャンネル分となります。
つまり出力ベクトルのチャンネル数はカーネルの数と同じになり、一般にはそこそこ多い数です。(128や256等、別に2のべき乗である必要はありませんが良く使われるようです。)
出力されたベクトルのチャンネルは元のR,G,Bのような意味ではなく、ネットワークが演算した何らかの特長量となります。(例えば、あるチャンネルは画像中のエッジ検出を行っているかもしれません。)
上でも述べた通り、入力ベクトルのチャンネル(前の層の出力ベクトルのチャンネルと同義)が複数ある場合には1つのカーネルに対しそれぞれ計算し、それらを合算します。
全結合層との違い
前述の通り、畳み込みという手法自体が画像認識で使用されているので、この手法が有効なのは極自然ですが、なぜこの畳み込み層が良いのかについて、全結合層との違いを説明したいと思います。
全結合層は字の通り入力側と出力側の各ベクトルをすべて結合する、ニューラルネットワークでは一番普通の層です。
すべてのベクトルをそれぞれ結合するので、実はこの層ではベクトルの位置に意味がなくなります。
(実際には全結合層は畳み込み演算を表現することができるので上手く学習できればベクトルの位置を考慮した重みとなるはずです。
しかし、今論じているのは学習を上手くいかせるための方法ですので、前提である上手く学習できればの部分がクリアできません。)
それに加えて、重みパラメータの数が全然違います。
例として28×28(×1)の画像(小さな画像です)に3×3の畳み込み演算を適用する場合を考えてみましょう。
畳み込み層が学習するパラメータは3×3=9個です。
対して全結合層では、同様のベクトルを出力するとするならば出力ベクトルは26×26×1なので、入力(28×28)× 出力(26×26×1)=529,984個の重みパラメータを学習することになります。
多すぎるパラメータは以前の記事で書いた過学習の状態につながります。
過学習を避け、学習の効率を良くするためには、パラメータの数は画像の特徴をしっかり捉えられる程度に多く、重複がない程度に少ないことが望ましいと言えます。
(このような状態をスパースな状態というらしいです。)
そのような観点で見ると、畳み込み層のカーネルは周囲の状況から画像の特徴を拾うことができ、かつパラメータの数が少ないということでとても良い学習性能を発揮できます。
プーリング(Pooling)層
プーリング層も、畳み込み層と同じく画像認識用の深層学習で良く用いられます。
畳み込み層とプーリング層でセットとして扱われることが割と多い印象です。
プーリング層では入力ベクトルをいくつかの範囲に分割し、それぞれ処理して出力ベクトルを出力します。
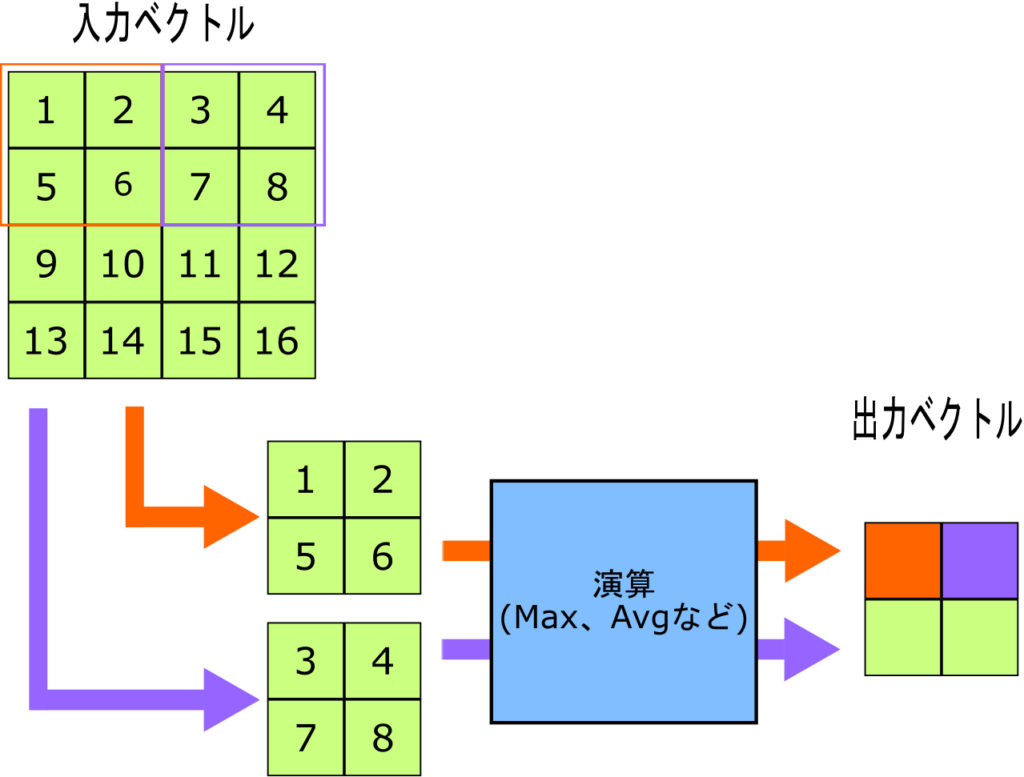
概要としては上の図のようになります。図では2×2でプーリングを行っています。
プーリング層にはいくつか種類がありメジャーなものとして最大値を取るMaxPoolingや、平均値を取るAveragePoolingが挙げられます。
入力ベクトルを2×2の範囲に分割し、MaxPoolingであれば4つのベクトル要素のうち最大の値を出力ベクトルの要素とします。
基本的にはPoolingをすることで出力ベクトルのサイズは小さくなります。
畳み込み層でチャンネルを増やし、その後のプーリング層でサイズを小さくする、というような使い方が多く、横にしたピラミッドのようなモデル概念図をよく見かけます。
図を見ると畳み込み層とよく似ています。違いとして、1つはベクトルの切り出し方が重複しないように切り出している点ですが、これは畳み込み層にもstrideと呼ばれる1個飛ばし、2個飛ばしのような使い方があるので、必ずしもそれがプーリング層の特徴ではありません。
もう1つの違いは、カーネルで表しずらい処理を行っている点ですが、これもAveragePoolingであればすべての要素を1/(カーネルサイズ)にしたカーネルで実現できます。
MaxPoolingはカーネルでの再現は難しそうです。
一番の違いは処理が決まっており、学習パラメータがないという点です。
上にも書いた通り、パラメータは少なく、それでいて画像の特徴を捉えられる処理が望ましいです。
プーリング層が広く使われているのはパラメータ無しでこの機能を実現しているからだと思います。
プーリング層の効果はある範囲の値をまとめて処理するモデルにすることで、微妙な画素のずれなどに強くなることだと言われています。
例えば画像がほんの1,2ピクセル横に移動しただけで判別ができなくなるようでは画像認識の精度は良いとは言えません。プーリング層はこのような微妙なずれや揺らぎを許容して、堅牢性の高い判別モデルの実現に役立っています。
ドロップアウト(Dropout)
これまで紹介した3つの手法のうち、2つが画像を主な対象とした手法であり、ReLUも活性化関数なので画像を含む多くの深層学習モデルで使用されています。
これらの手法により画像に対する深層学習の精度はとても良いものになっています。
一方で画像以外を対象としたネットワークを考えたときに使用できる手法で有効なものの一つがドロップアウトです。
ドロップアウトは全結合層等のネットワークでニューロンの一部を無効化して学習を行う手法です。
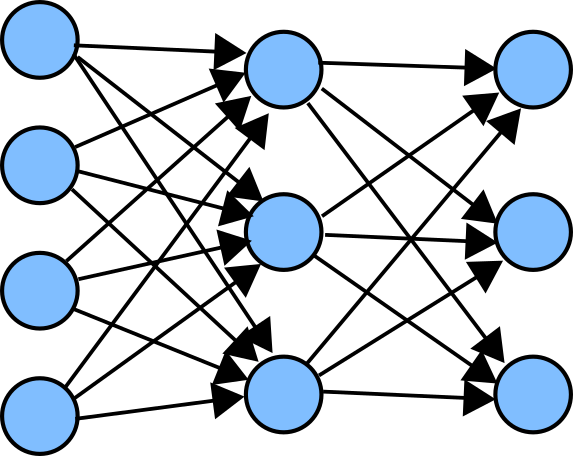

上の図は簡単な全結合ネットワークの例です。
左の図は元の全結合ネットワークを示しています。右の図はネットワーク中の一部のニューロンを無効化したものです。ニューロンを無効化することでネットワークの形状が変化しています。
ニューラルネットワーク学習は繰り返し行われますが、学習の度にランダムにニューロンを無効化します。無効化するニューロンの数は層内の割合などで指定される場合が多いです。
ドロップアウトはアンサンブル学習に似た効果が得られると言われています。
アンサンブル学習は複数のモデルを使用して推定を行い、各モデルの結果を平均するなどして安定した結果を得る手法です。
上でも説明した通り、モデルのパラメータは少ない方が学習が上手くいきやすいです。一方で、一般にはモデルのパラメータが多い方が複雑なモデルを表現できるようになります。
ドロップアウトは複雑で学習が難しいモデルに対してパラメータを限定して局所的な学習を行い、これらを統合して全体を学習するという手法になります。
ドロップアウトは元々全結合層のモデルを学習するために提案されたようで、メジャーなモデルでは全結合層とセットで使用されている場合が多いようです。
実際は畳み込み層に対して適用しても効果があるようです。
バッチ正規化(Batch Normalization)
以前の記事には書きませんでしたが、いろいろ調べる中で学習の安定化に大きく寄与している手法としてバッチ正規化が挙げられている場合が多かったので追加で説明します。
バッチ正規化は、ある層の出力を、バッチ(1回に学習計算をさせるデータのまとまり)ごとに平均0、分散1の分布となるように正規化する手法です。
ニューラルネットワークは出力層に近い側から学習をしていくので、出力層に近い側の層が誤差を基に学習を行っても、その後にその層にデータを入力する一つ上の層が学習された結果、それぞれが良いと思われる方向に学習されて行き違いが起こる場合があるようです。
これを避けるために、層に入力されるデータの分布を一定にすることで学習が安定するということらしいです。
このバッチ正規化はメジャーなモデルでもよく見かける手法で、一部のモデルでは前述のドロップアウト無しでも深層学習モデルの学習に成功した例もある、強力な手法のようです。
以上、深層学習が可能となった大きな要因と考えられる、多くのモデルの中で広く用いられる手法を説明しました。
実際にはこれらを組み合わせたりしてさらに強力で効果的な手法がいくつも提案されています。
(ネットワークがモジュール化され、名前がついていたりします。)
その根底には今回説明したような手法があるというのが、私がこれまで少ないながらいくつかのメジャーなモデルを見てきた印象です。
次回以降もう少し実践寄りの、実際に深層学習をやってみたい方向けの内容を書いていこうかと思います。