ニューラルネットワークは機械学習の中の一手法ですが、ほかの機械学習手法で問題となる、特徴ベクトルの抽出まで含んだ学習を行うことができる手法として注目を浴びました。
実はこのニューラルネットワーク、これまでの研究の流れの中で、何度かブームと呼ばれる注目期間があり、現在は第3次ニューラルネットワークブームに当たるようです。
第2次ニューラルネットワークブームとその問題点
第2次ニューラルネットワークブームはバックプロパゲーションの定式化により、多層化ネットワークの学習方法が一般化されたことで起きました。
実はニューラルネットワークは1層ではごく単純なXOR(2つの入力のうち一つだけが1、他が0の時出力が1となる論理演算子)を実現することができません。
この問題はニューラルネットワークを2層重ねることで解決できるとされていましたが、この2層のネットワークを学習する方法が第2次ブーム以前は理論的に定式化されていませんでした。
当然、多層ネットワークの学習方法が定式化されたことにより問題は解決、第2次ニューラルネットワークブームが起きます。
多層化ネットワークが学習できる、と聞けば当然層をどんどん増やしていけばネットワークの性能がどんどん向上していくと期待します。
しかし、実際には多層化(深層化)したニューラルネットワークは学習が上手く進まず、むしろ性能が悪化するというものでした。
多層化ネットワークの学習で問題と考えられるのは以下の3つです。
- 勾配消失
- 過学習
- 局所解
勾配消失
勾配消失はその名の通り、学習の中で勾配が消失する問題です。
ニューラルネットワークの学習は出力層から誤差を計算し、前の層にその誤差を伝えて学習データ入力とは逆順に誤差計算をしていきます。
この誤差計算時に、各層の活性化関数の微分を誤差に乗算(掛け算)する計算があります。
ここで、第3次ブーム以前によく使用されていた活性化関数であるロジスティックシグモイド関数(sigmoid)とtanh関数、それぞれの導関数(微分)は下図のような形をしています。
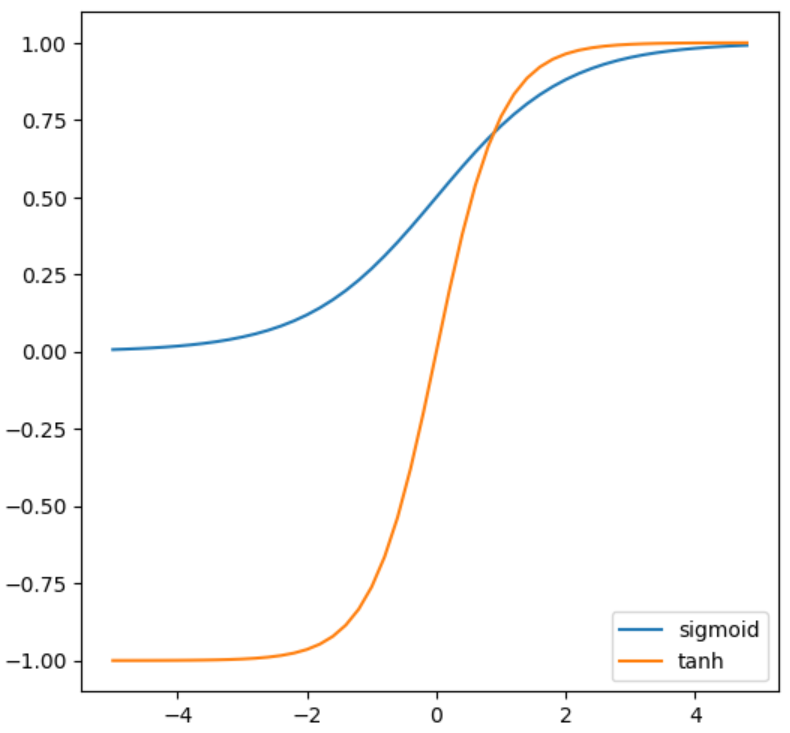
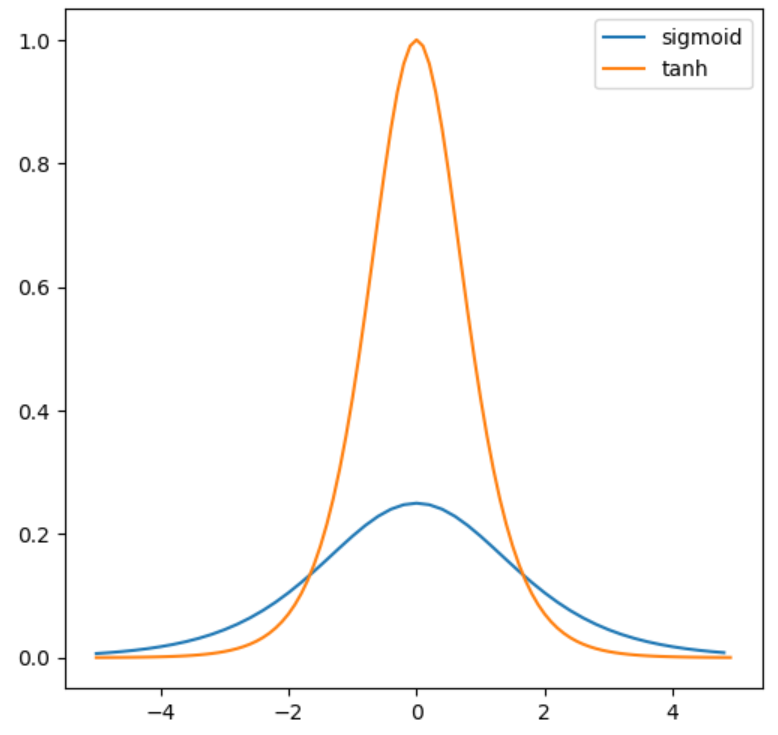
ロジスティックシグモイド関数の微分は0~0.25とかなり小さいです。これを各層の活性化関数として用いた場合、0.25の(層数)乗を誤差に乗算していることになるので、上の層に行くにつれて伝達されてくる誤差はとても小さくなります。
ニューラルネットワークの学習は求められた各層の誤差を基に行われるので、誤差が小さくては学習が上手く進みません。
この問題を改善するために活性化関数としてtanh関数を用いる手法が提案され、性能は改善されましたが、tanh関数も0付近以外での微分が小さく、まだまだ十分ではありませんでした。
過学習
過学習はニューラルネットワークのみならず、機械学習全般で問題となる場合があります。
例えば、簡単なn次関数の回帰問題を考えます。
下図のようなデータがあるとします。
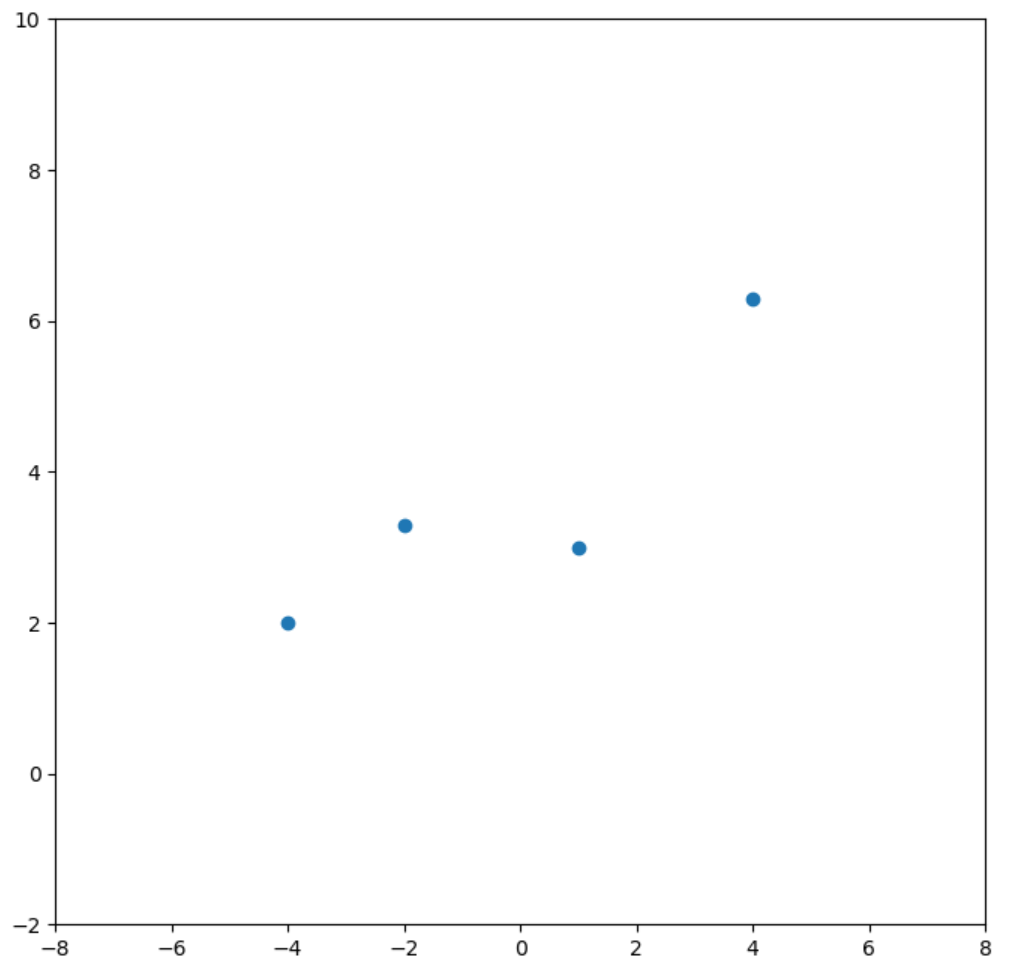
これを1次、2次、3次関数でそれぞれ誤差最小二乗法による近似曲線(回帰曲線)を求めます。
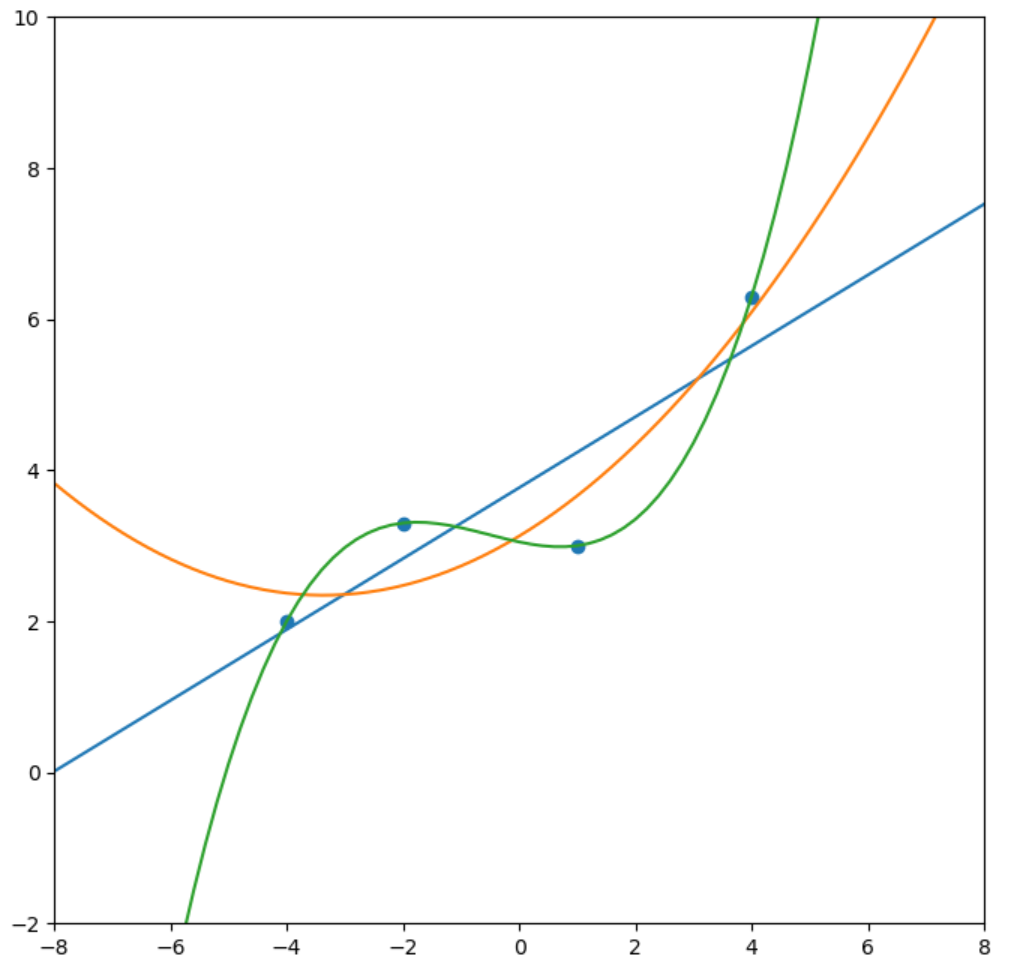
3次曲線ではすべてのデータに合致する曲線が得られました。
しかし、この3次の曲線は精度の良い回帰曲線でしょうか。
散布図の各データには誤差がのっている場合が考えられますので、直線による近似でも十分ではないかと思います。
例えば今回訓練データに入っていないx=-6などの結果を予測する場合には、1次、2次、3次で結果が大きく変わってしまい、直感的に良い結果とは大きく異なってしまいます。
このように推測モデルの表現能力を高めすぎたり、学習の進度を進めすぎたりすることで、訓練データに特化したモデルとなってしまい、未知のデータへの予測結果が逆に悪くなってしまうのが過学習です。
機械学習全般ではこれを避けるために学習用のデータと評価用のデータを分けて、学習の結果を評価するのが基本となります。
局所解
局所解は勾配などを用いて逐次的に解を探索する手法でよく現れる問題です。
ニューラルネットワークで解きたい問題は当然複雑な非線形問題が主ですので、そのパラメータ空間は下図のようにボコボコになっていることが想像できます。
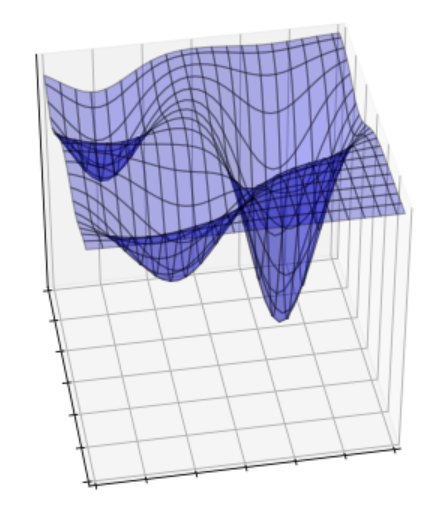
最小値を見つける最小化問題であるとして、上の図では極小となる(極近い周囲のどの場所よりも小さい)場所が3か所あります。
探索は初期解を基に勾配(傾き)などにより方針を与えられて最小値を探していきますので、例えば初期解が図の左側に配置されると、左側の2つのどちらかに向かって探索が進んで行きそうです。
対策として、機械学習や最適化問題の分野では初期値をランダムにして複数回の探索・学習を行ったり、探索にランダム要素を入れて極小範囲から抜け出すなどの方法がとられます。
ニューラルネットワークで取り扱うパラメータ数はかなり多く、パラメータ空間も複雑ですので、局所解が多数存在することが想定されます。
深層学習
現在の人工知能ブームの実態は何かと言えば、深層学習ですが、この深層学習はこれまで説明したニューラルネットワークを多層化(深層化)したものです。
前述した通り、ニューラルネットワークの深層化には問題が多く、これまでは上手く学習させることができませんでした。
これらの問題をすべて解決したのが・・・!!!と言いたいところですが、実のところ私にはよく分かりません。
少し勉強したところでは、様々な人たちの色々な手法的アプローチの結果、上手く学習できる方法が見つかった。というのが私の感触です。
そんな中でも広く用いられて、これを使えば割と上手く学習できるという手法がいくつかあります。
- ReLU (活性化関数)
- 畳み込み層
- Pooling層
- Dropout層
これ以外にも数多くの革新的なモジュールなどが提案され、性能は日々向上していますが、その多くがこれらの手法を組み合わせて構成されており、それらモジュールの学習精度を確保するための大きな要因になっているのではないかと思います。
各手法については次回簡単に説明したいと思います。